Quảng cáo
2 câu trả lời 2626
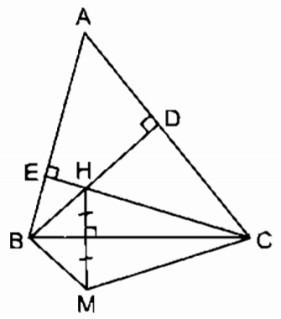
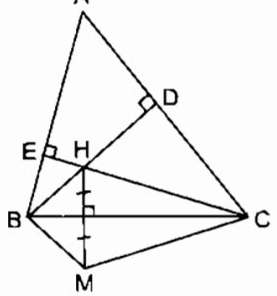
a. Vì M đối xứng với H qua trục BC
⇒ BC là đường trung trực của HM
⇒ BH = BM ( tính chất đường trung trực)
CH = CM ( tính chất đường trung trực)
Suy ra: ∆ BHC = ∆ BMC (c.c.c)
b. Gọi giao điểm BH với AC là D, giao điểm của CH và AB là E
H là trực tâm của ∆ ABC
⇒ BD ⊥ AC, CE ⊥ AB
Xét tứ giác ADHE ta có:
góc DHE=360 độ −( góc A+góc EHD+góc AEH )
=360 độ −(60 độ +90 độ +90 độ )=120 độ
góc BHC=góc DHE (đối đỉnh)
∆ BHC = ∆ BMC (chứng minh trên)
⇒ góc BMC= góc BHC
Suy ra:góc BMC=góc DHE=120 độ
Quảng cáo
Câu hỏi hot cùng chủ đề
-
100165
-
Hỏi từ APP VIETJACK50388
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức MH2=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
42673