Quảng cáo
2 câu trả lời 9211
Bước 1: Quy đồng hai vế
Biến đổi vế trái:
Vế trái:
![]()
Nhân cả tử và mẫu của phân thức với 1 + cosx (mẫu số vế phải):
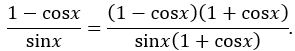
Sử dụng hằng đẳng thức : (a - b)(a + b) = a2 - b2:
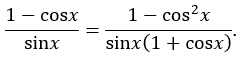
Do 1 - cos2x = sin2x (đẳng thức lượng giác cơ bản), ta có:
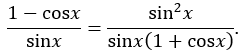
Rút gọn sinx ở tử và mẫu:
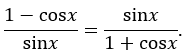
Bước 2: So sánh với vế phải
Vế phải cũng là:
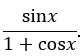
Như vậy, hai vế bằng nhau:
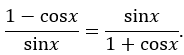
Kết luận
Phương trình đã được chứng minh đúng.
\[\begin{array}{l}
\frac{{1 - \cos x}}{{\sin x}} = \frac{{sinx}}{{1 + \cos x}}\\
co:\\
{\sin ^2}x + {\cos ^2}x = 1\\
= > {\sin ^2}x = 1 - {\cos ^2}x\\
= > \sin x.\sin x = (1 - \cos x)(1 + \cos x)\\
= > \frac{{1 - \cos x}}{{\sin x}} = \frac{{\sin x}}{{1 + \cos x}}\\
= > Dpcm
\end{array}\]
Quảng cáo
Bạn muốn hỏi bài tập?


