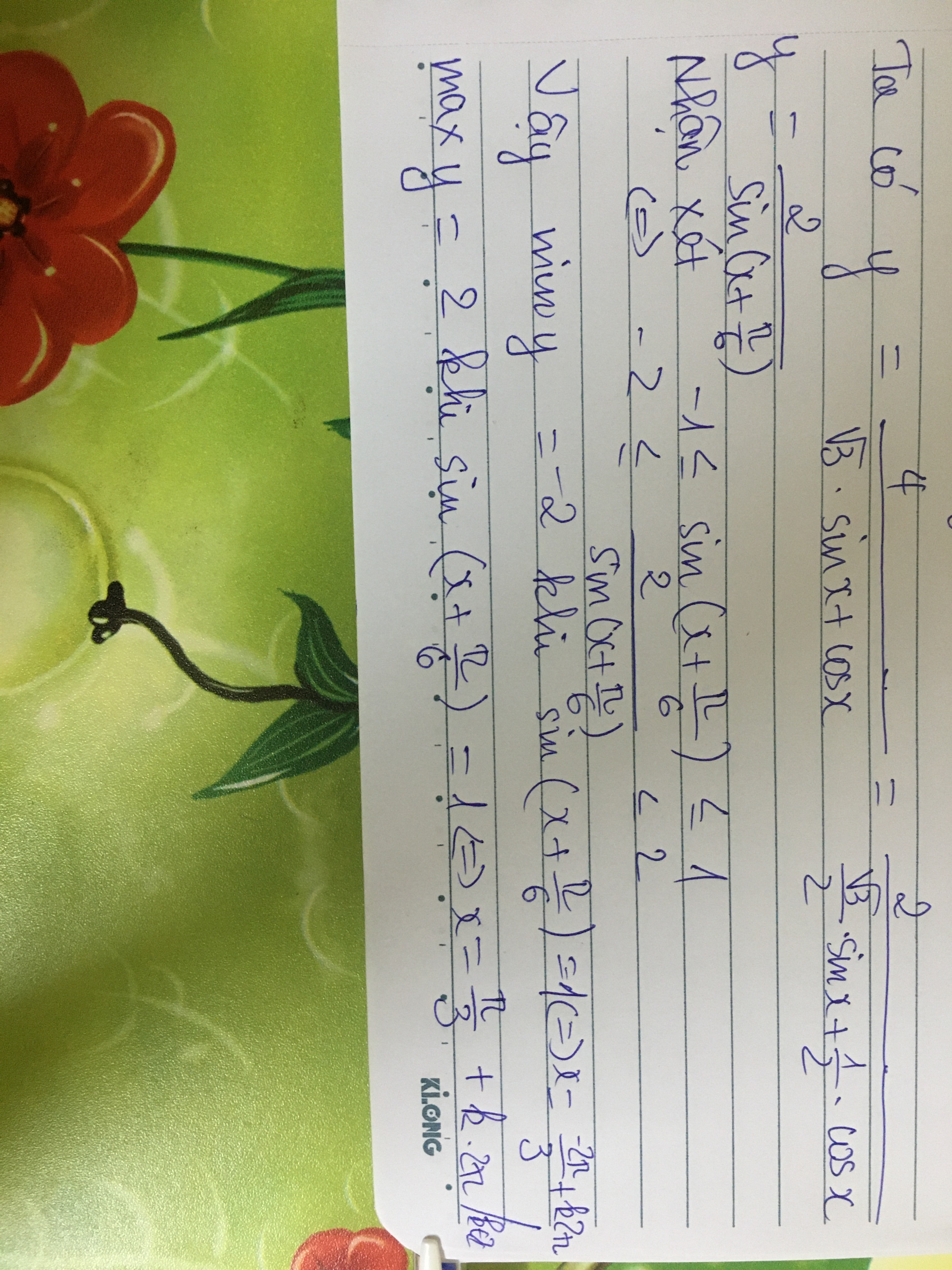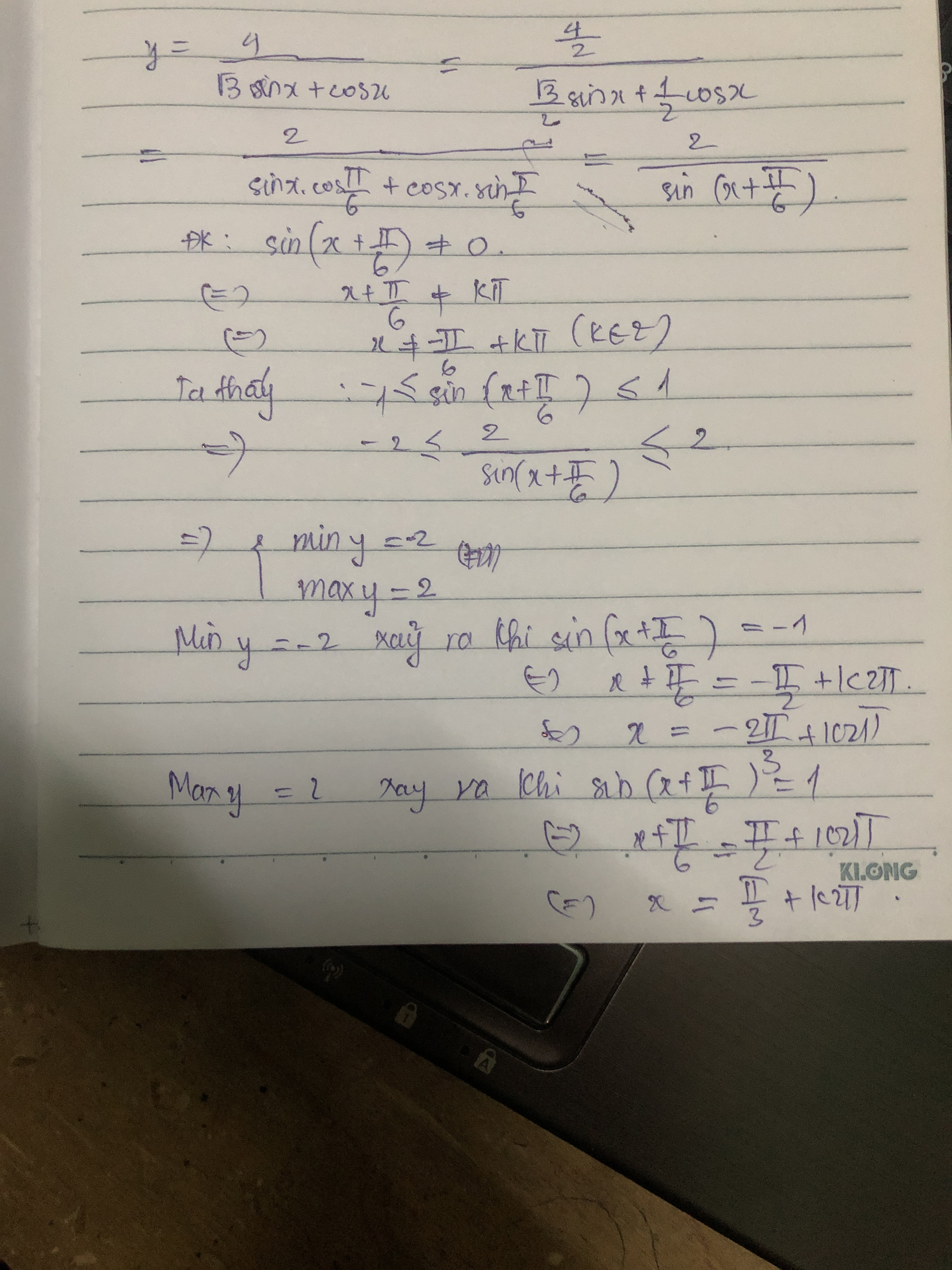Quảng cáo
3 câu trả lời 958
\[\begin{array}{l}
y = \frac{4}{{\sqrt 3 \sin x + \cos x}}\\
= \frac{2}{{\frac{{\sqrt 3 }}{2}\sin x + \frac{1}{2}\cos x}}\\
= \frac{2}{{\sin x.\cos \frac{\pi }{6} + \cos x.\sin \frac{\pi }{6}}}\\
= \frac{2}{{\sin (x + \frac{\pi }{6})}}\\
do: - 1 \le \sin (x + \frac{\pi }{6}) \le 1\\
= > \left[ \begin{array}{l}
\frac{2}{{\sin (x + \frac{\pi }{6})}} \ge 2\\
\frac{2}{{\sin (x + \frac{\pi }{6})}} \le - 2
\end{array} \right.
\end{array}\]
=> Không tồn tại min; max của hso
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
Thành viên hăng hái nhất trong tuần
-
2235 điểm
-
I miss you
2045 điểm
-
𓇼 ⋆.˚annabelle⋆.˚ 𓇼 1260 điểm
-
Judy Hopps
1100 điểm
-
bích hồng nguyễn 760 điểm
-
`color{red}text{HuyTùng`
530 điểm
-
zai đẹp siu
490 điểm
-
lọ hà nội
440 điểm
-
dũng ngon hơn ok
405 điểm
-
Haruto[pad] 395 điểm
-
chê ng tốt chốt ng tồi.
365 điểm
-
n.t.an
300 điểm
-
⋅˚₊‧ ଳ⋆.࿔*:･𝙇ệ_ဗီူ_𝙥𝙝𝙪_ဗီူ_𝙣𝙝â𝙣⋅˚₊‧ ଳ⋆.࿔*:･
245 điểm
-
minhxinhquama
190 điểm
-
✿ 𝓝𝓪̂́𝓶 🍄
180 điểm
Rút gọn
Bài viết mới nhất Lớp 11
-
3 năm trước3535
-
3 năm trước3376
Gửi báo cáo thành công!
