a)

$\begin{array}{l} Sinx + sin3x + sin5x + sin7x = 0\\ \Leftrightarrow (\sin x + \sin 7x) + (\sin 3x + \sin 5x) = 0\\ \Leftrightarrow 2\sin 4x.\sin 3x + 2\sin 4x.\sin x = 0\\ \Leftrightarrow 2\sin 4x(\sin 3x + \sin x) = 0\\ \Leftrightarrow 2\sin 4x(2\sin 2x.\sin x) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin 4x = 0\\ \sin 2x = 0\\ \sin x = 0 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} 4x = k\pi \\ 2x = k\pi \\ x = k\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = \frac{{k\pi }}{4}\\ x = \frac{{k\pi }}{2}\\ x = k\pi \end{array} \right.\\ \Leftrightarrow x = \frac{{k\pi }}{4}(k \in Z) \end{array}$

b)

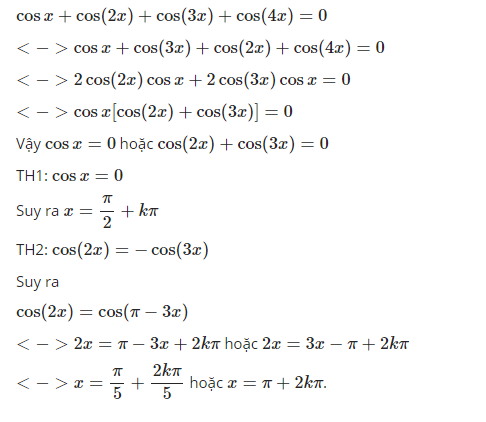
sinx + sin3x + sin5x + sin7x = 0

(sinx + sin7x) + (sin3x + sin5x) = 0

2sinx (8x / 2) * cos (-6x / 2) + 2sin (8x / 2) * cos (-2x / 2) = 0

2sin4x * cos3x + 2sin4x * cosx = 0

2sin4x (cos3x + cosx) = 0

2sin4x * 2cos ((3x + x) / 2) * cos ((3x-x) / 2) = 0

4sin4x * cos (4x / 2) * cos (2x / 2) = 0

4sin4x * cos2x * cosx = 0

sin4x = 0 hoặc cos2x = 0 hoặc cosx = 0

4x =k2pi

2x = pi/ 2 + kpi

x = pi/2+kpi

<=>

 x = kpi/2, x = P / 4 + kpi/2, x = P / 2 +kpi

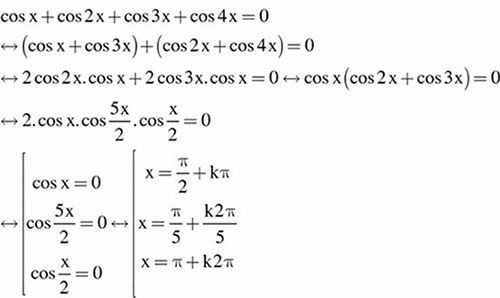
câu a
Cái này chỉ cần áp dụng 2 CT:
sin3x - sinx = 2cos2x.sinx
và cos2x = 2cosx - 1 là ra
2cos2x.sinx + 2sinx.cosx = 0
<=> 2sinx( cos2x + cosx) = 0
<=> 2sinx( 2cos^2x - 1 + cosx) = 0
<=>[sinx=0
      [2cos^2x-1+cosx=0
câu b 
cosx + cos2x +cos3x + cos4x=0 
cosx + cos3x +cos2x+cos4x=0 
2cos2xcosx + 2cos3xcosx=0 
cosx(cos2x+cos3x)=0 
cosx=0 hoặc cos2x+cos3x=0 
x = pi/2 +kpi 
hoặc cos2x= -cos3x 
cos2x= cos(pi-3x) 
x= pi/5 + k2pi/5 hoặc x=pi+ k2pi 
vậy họ nghiệm là x= pi/2 + kpi , x= pi/5 + k2pi/5 , x= pi +k2pi