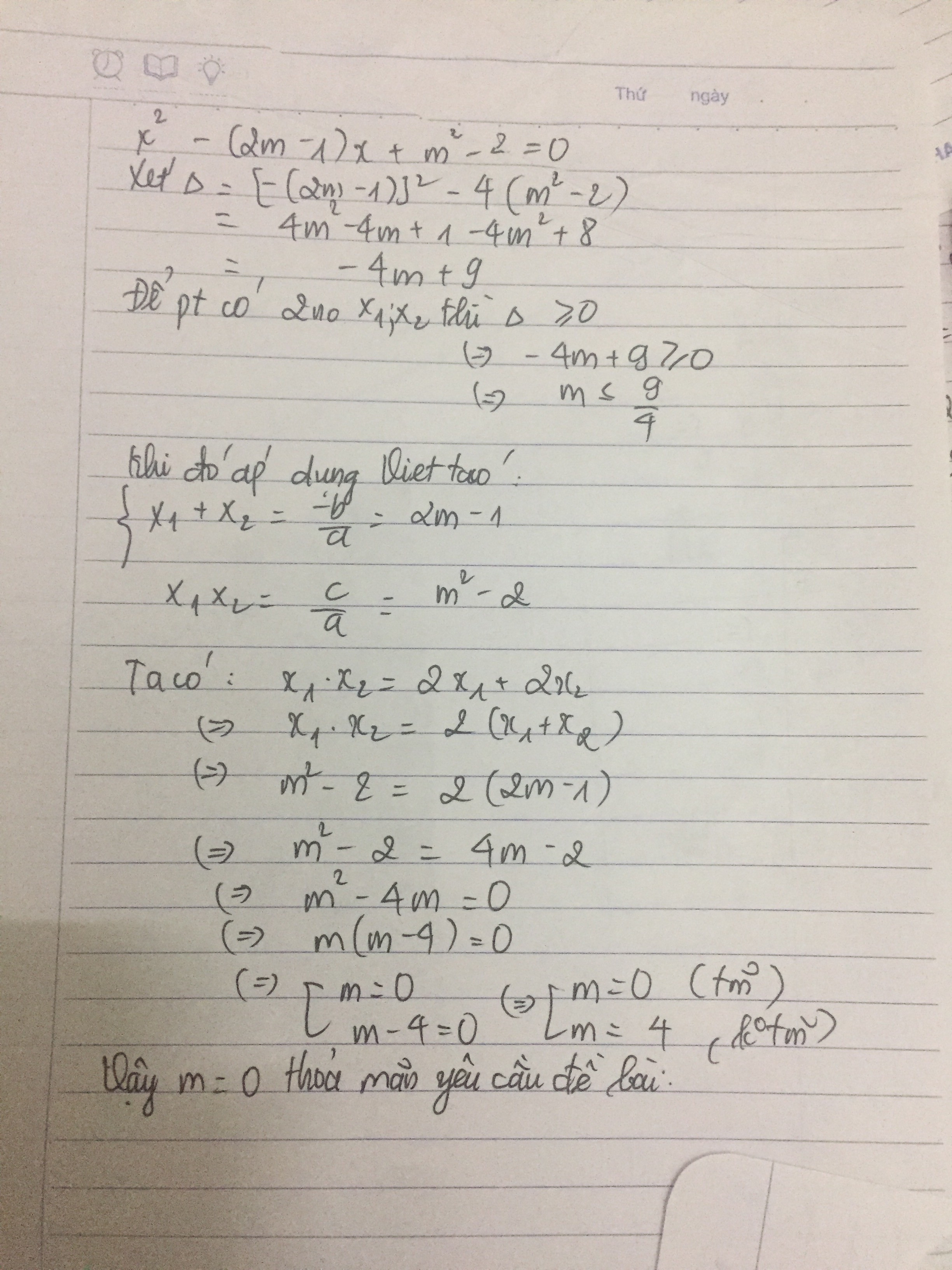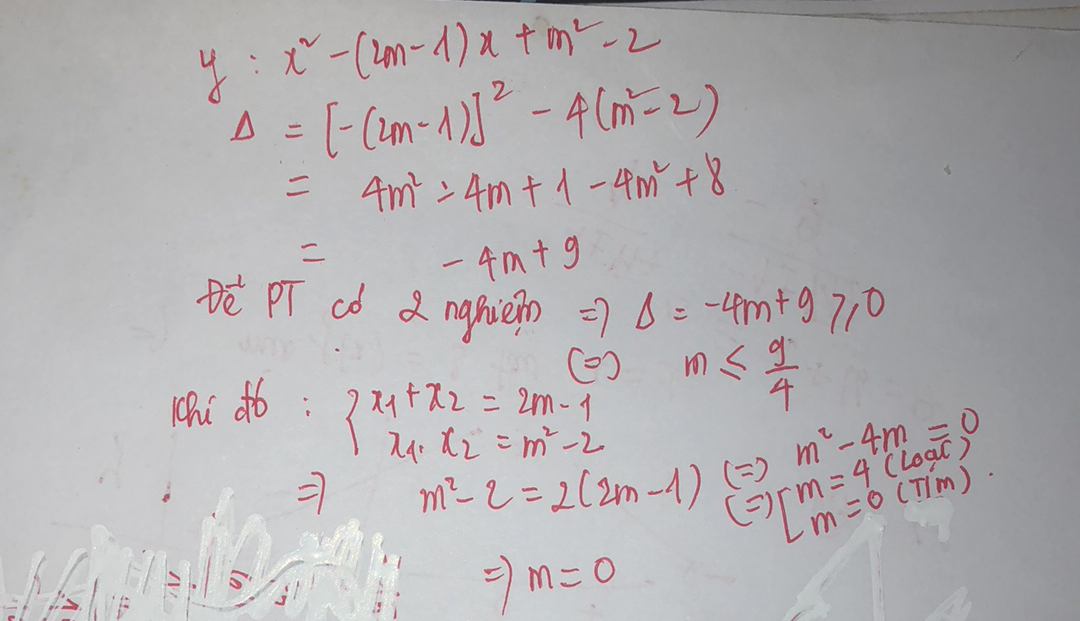x²-(2m-1)x+m²-2=0
Tìm m để pt có nghiệm x1x2 thỏa mãn:x1.x2=2x1+2x2
Quảng cáo
4 câu trả lời 2427
Để phương trình có hai nghiệm phân biệt thì $\Delta \geq 0$
$\Delta=(2m-1)^2+4(m+2)$
$\Delta =-4m+9 \geq 0$
$\Leftrightarrow m \leq \dfrac94$
Áp dụng định lý Vi-et ta có: $\begin{cases}x_1+x_2=2m-1\\x_1x_2=m^2-2\end{cases}$
$x_1x_2=2x_1+2x_2$
$\Leftrightarrow m^2-2=2(2m-1)$
$\Leftrightarrow m^2-2=4m-2$
$\Leftrightarrow m^2-4m=0$
$\Leftrightarrow m(m-4)=0$
$\Leftrightarrow \left[\begin{array}{l}m=0\\m=4\ (ktm)\end{array}\right.$
Vậy $m=0$ thì thỏa mãn yêu cầu bài toán.
Đáp án: $m=0$
Giải thích:
${{x}^{2}}-\left( 2m-1 \right)x+{{m}^{2}}-2=0$
$\Delta ={{\left[ -\left( 2m-1 \right) \right]}^{2}}-4\left( {{m}^{2}}-2 \right)$
$\Delta =4{{m}^{2}}-4m+1-4{{m}^{2}}+8$
$\Delta =-4m+9$
Để phương trình có nghiệm thì $\Delta \ge 0\,\,\Leftrightarrow \,\,-4m+9\ge 0\,\,\Leftrightarrow \,\,m\le \dfrac{9}{4}$
Khi đó, theo hệ thức Vi-et, ta có: $\begin{cases}x_1+x_2=2m-1\\x_1x_2=m^2-2\end{cases}$
$\bullet \,\,\,\,\,{{x}_{1}}{{x}_{2}}=2{{x}_{1}}+2{{x}_{2}}$
$\Leftrightarrow {{x}_{1}}{{x}_{2}}=2\left( {{x}_{1}}+{{x}_{2}} \right)$
$\Leftrightarrow {{m}^{2}}-2=2\left( 2m-1 \right)$
$\Leftrightarrow {{m}^{2}}-2=4m-2$
$\Leftrightarrow {{m}^{2}}-4m=0$
$\Leftrightarrow m\left( m-4 \right)=0$
$\Leftrightarrow\left[\begin{array}{l}m=0\,\,\,\left(tmdk\right)\\m=4\,\,\,\left(ktmdk\right)\end{array}\right.$
Vậy với $m=0$ thì ${{x}_{1}}{{x}_{2}}=2{{x}_{1}}+2{{x}_{2}}$
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13676
Đã trả lời bởi chuyên gia
13676 -
 Đã trả lời bởi chuyên gia
13621
Đã trả lời bởi chuyên gia
13621 -
 Đã trả lời bởi chuyên gia
6429
Đã trả lời bởi chuyên gia
6429 -
 Đã trả lời bởi chuyên gia
6148
Đã trả lời bởi chuyên gia
6148 -
6111
-
 Đã trả lời bởi chuyên gia
5440
Đã trả lời bởi chuyên gia
5440 -
 Đã trả lời bởi chuyên gia
4451
Đã trả lời bởi chuyên gia
4451