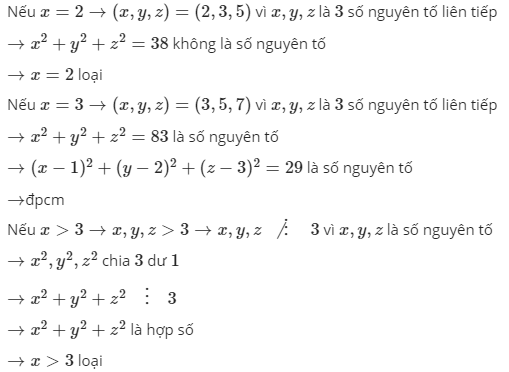Cho 3 số nguyên tố liên tiếp x, y, z thỏa mãn x<y<z và là một số nguyên tố. Chứng minh: cũng là một số nguyên tố.
Quảng cáo
2 câu trả lời 8293
1 năm trước
Nếu x = 2 -> (x, y, z) = (2, 3, 5)
vì x, y, z là 3 số nguyên tố liên tiếp
-> x2 + y2 + z2 = 38 không là số nguyên tổ
-> x = 2 loại
Nếu x = 3 -> (x, y, z) = (3, 5, 7)
-> x = 2 loại
Nếu x = 3 -> (x, y, z) = (3, 5, 7)
vì x, y, z là 3 số nguyên tố liên tiếp
-> x2 + y2 + z2 = 83 là số nguyên tố
+ (x - 1)2 + (y - 2)2 + (z - 3)2 = 29 là số nguyên tố
+ (x - 1)2 + (y - 2)2 + (z - 3)2 = 29 là số nguyên tố
(đpcm)
Nếu x > 3 -> x, y, z > 3 -> x, y, z /: 3
Nếu x > 3 -> x, y, z > 3 -> x, y, z /: 3
vì x, y, z là số nguyên tố
-> x2, y2, z2 chia 3 dư 1
+ a2 + y2 + 22 : 3 -> x2 + y2 + z2 là hợp số
+ x > 3 loại
+ a2 + y2 + 22 : 3 -> x2 + y2 + z2 là hợp số
+ x > 3 loại
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171
Thành viên hăng hái nhất trong tuần
-
우옌🖤 해영 ✨
1810 điểm
-
Sori
1745 điểm
-
사랑해요😘
1190 điểm
-
Dương Nguyễn
1140 điểm
-
`color{blue}text{HuyTùng☢`
925 điểm
-
그림 그리기를 좋아하지만, 직업이 허락하지 않아요😞
875 điểm
-
하루토 [팜 안 둥]
850 điểm
-
돈이없다 💸😭
845 điểm
-
`d.`
805 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
785 điểm
-
🌷김은✨
630 điểm
-
Bích Hồng 625 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
585 điểm
-
jamJames 🥵👍
555 điểm
-
''e thik biker hơn a''
480 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8220
-
3 năm trước7732
-
3 năm trước6571
-
3 năm trước6459
-
3 năm trước6291
Gửi báo cáo thành công!
