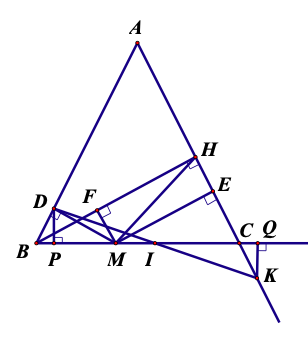
Cho tam giác ABC cân tại A, BH vuông góc AC tại H. Trên cạnh BC lấy điểm M bất kì (M khác B và C). Gọi D, E, F là chân đường vuông góc hạ từ M đến AB, AC, BH.
a) Chứng minh: ∆DBM = ∆FMB.
b) Chứng minh khi M chạy trên cạnh BC thì tổng MD + ME có giá trị không đổi.
c) Trên tia đối của tia CA lấy điểm K sao cho CK = EH.
Chứng minh BC đi qua trung điểm của đoạn thẳng DK.
Quảng cáo
2 câu trả lời 7831

Hải Nguyên
· 3 năm trước
nói rõ ra câu a đc khum ạ.
hieuminh luu
· 1 năm trước
Đáp án a như sau:
hieuminh luu
· 1 năm trước
Vì tam giac dmp vuông tai d => goc dmp+goc mbd=90⁰
hieuminh luu
· 1 năm trước
Tam giac fbm vuông tại f =>=>fmb+mbf=90⁰
hieuminh luu
· 1 năm trước
=> góc dmp =g fbm
hieuminh luu
· 1 năm trước
Rồi xét tam gíacs
hieuminh luu
· 1 năm trước
Câu b có thể làm cạnh bằng nhau
hieuminh luu
· 1 năm trước
=>khi đổi vị trid vẫn thế
Lập luận được hoặc
Chứng minh được
Theo câu ta có: (1)
Chứng minh: (2)
Từ (1) và (2) suy ra
Vẽ tại P, tại Q
+) Chứng minh:
+)Chứng minh (cạnh tương ứng)
+)Chứng minh
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757
Gửi báo cáo thành công!


