Giải phương trình
Quảng cáo
1 câu trả lời 9476
Giải phương trình:
![]()
Bước 1: Đặt ẩn phụ
Quan sát các mẫu số, ta thấy:
![]()
có dạng x2 - 2x + k với k = 2,3,4. Do đó, đặt:
![]()
Khi đó:
![]()
Phương trình trở thành:
![]()
Bước 2: Quy đồng mẫu số
Quy đồng mẫu số của phương trình, ta được:
![]()
Loại bỏ mẫu số (vì các mẫu t + 2, t + 3, t + 4 ), ta được:
![]()
Bước 3: Khai triển và rút gọn
Khai triển từng số hạng: -(t + 3)(t +4) = t2 + 4t + 3t + 12 = t2 + 7t + 12, -2(t + 2)(t + 6)(t2 + 3t + 2t + 6) = 6(t2 + 5t + 6) = 6t2 + 30t + 36
Thay vào phương trình:
![]()
Cộng các số hạng ở vế trái:
![]()
Phương trình trở thành:
![]()
Bước 4: Chuyển vế và giải phương trình bậc hai
Chuyển tất cả về một vế:
![]()
Rút gọn:
![]()
Chia cả hai vế cho -1:
![]()
Giải phương trình bậc hai bằng công thức nghiệm:
![]()
với a = 3, b = 11, c = 8. Thay vào:
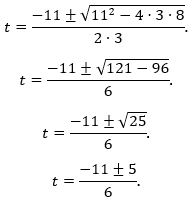
Tính hai nghiệm:
![]()
Bước 5: Trả lại ẩn x
Với t = x2 - 2x, ta giải hai phương trình:
1. Khi t = -1:
![]()
2. Khi ![]() :
:
![]()
Giải phương trình bậc hai này:
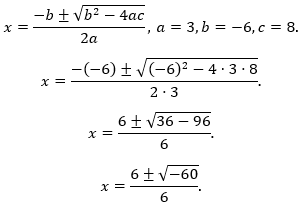
Phương trình này vô nghiệm vì ![]() không xác định trên tập số thực.
không xác định trên tập số thực.
Kết luận
Nghiệm của phương trình là:
![]()
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


