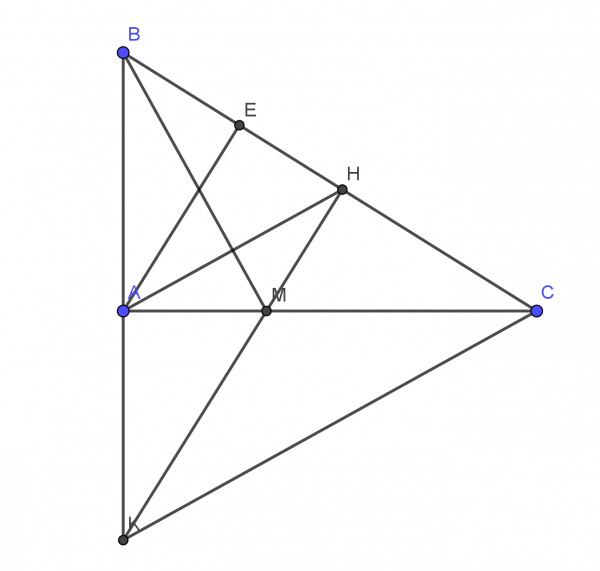
a) Xét tam giác vuông ABC có:

\(\begin{array}{l}
B{C^2} = A{B^2} + A{C^2}\\
 =  > AC = \sqrt {{5^2} - {3^2}}  = 4(cm)
\end{array}\)

b) Xét tam giác ABM và tam giác HBM có:

Góc ABM=góc HBM( do BM là tia phân giác của góc BAC)

BM chung

Góc AMB= góc HMB( do Góc BAM=góc BHM=90)

=>Tam giác ABM=tam giác HBM

=> AB=HB

=>Tam giác ABH cân tại B

c) ta có góc ABM< góc ABC

=> AM<AC

d) ta có tam giác ABM=tam giác HBM

=> AM=HM

Xét tam giác AMK và tam giác HMC có:

AMK=HMC(đối đỉnh)

AM=HM

Góc MAK=góc MHC=90

=> Tam giác AMK=tam giác HMC

=>MK=MC

=>Tam giác MKC cân tại M

e) Ta có: tam giác ABH cân tại B

=>Góc BAH=góc BHA

=>90-góc BAH=90-góc BHA

=> góc BAC-góc BAH=góc AEH-góc BHA

=>Góc HAC=góc EAH

=> AH là tia phân giác của góc EAC.

a) Xét tam giác vuông ABC có:

AC=4

b) Xét tam giác ABM và tam giác HBM có:

Góc ABM=góc HBM( do BM là tia phân giác của góc BAC)

BM chung

Góc AMB= góc HMB( do Góc BAM=góc BHM=90)

=>Tam giác ABM=tam giác HBM

=> AB=HB

=>Tam giác ABH cân tại B

c) ta có góc ABM< góc ABC

=> AM<AC

d) ta có tam giác ABM=tam giác HBM

=> AM=HM

Xét tam giác AMK và tam giác HMC có:

AMK=HMC(đối đỉnh)

AM=HM

Góc MAK=góc MHC=90

=> Tam giác AMK=tam giác HMC

=>MK=MC

=>Tam giác MKC cân tại M

e) Ta có: tam giác ABH cân tại B

=>Góc BAH=góc BHA

=>90-góc BAH=90-góc BHA

=> góc BAC-góc BAH=góc AEH-góc BHA

=>Góc HAC=góc EAH

=> AH là tia phân giác của góc EAC.

a) *Xét ΔABC vuông tại A có : AB² + AC² = BC²(Định lý Pytago)

Mà AB = 3cm ; BC=5cm(gt)

⇒      3² + AC² = 5²

⇒    9   +  AC² = 25

⇒             AC² = 25 - 9 = 16

⇒               AC = 4

Vậy cạnh AC = 4cm

b)*Xét ΔBAM vuông tại A có : ∠ABM + ∠AMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

*Xét ΔBHM vuông tại H có : ∠HBM + ∠HMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

⇒ ∠ABM + ∠AMB = ∠HBM + ∠HMB

Mà ∠ABM = ∠HBM( tia pg góc B cắt AC tại M)

⇒  ∠AMB = ∠HMB

*Xét ΔBAM và ΔBHM

Ta có : ∠AMB = ∠HMB(c/m t)

              Chung cạnh BM

              ∠ABM = ∠HBM(gt)

⇒ΔBAM = ΔBHM(g-c-g)

⇒ BA = BH (2 cạnh tương ứng)

⇒ΔABH cân tại B(Định nghĩa Δ cân)

c)*Xét ΔBAM và Δ BMC có:

            ∠ABM = ∠HBM(gt)

              Chung cạnh BM

              AB < BC( vì 3 cm < 5cm)

⇒  ΔBAM < ΔBMC(qh giữa góc và cạnh của Δ)

⇒ AM < MC(2 cạnh t/ứng)

d)*Xét ΔAKM và ΔMCK

Ta có: ∠KAM = ∠MHC(=90độ vì MH ⊥ BC ; ΔABC vg tại A)

            AM = AH(2 cạnh t/ứng do ΔBAM = ΔBHM)

            ∠AMK = ∠HMC( 2 góc đối đỉnh)

⇒ΔAKM = ΔMCK(g-c-g)

⇒MK = MC(2 cạnh t/ứng)

⇒ΔMKC cân tại M(đ/n Δ cân)

Câu e bn thông cảm cho mk nhé

a) *Xét ΔABC vuông tại A có : AB² + AC² = BC²(Định lý Pytago)

Mà AB = 3cm ; BC=5cm(gt)

⇒      3² + AC² = 5²

⇒    9   +  AC² = 25

⇒             AC² = 25 - 9 = 16

⇒               AC = 4

Vậy cạnh AC = 4cm

b)*Xét ΔBAM vuông tại A có : ∠ABM + ∠AMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

*Xét ΔBHM vuông tại H có : ∠HBM + ∠HMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

⇒ ∠ABM + ∠AMB = ∠HBM + ∠HMB

Mà ∠ABM = ∠HBM( tia pg góc B cắt AC tại M)

⇒  ∠AMB = ∠HMB

*Xét ΔBAM và ΔBHM

Ta có : ∠AMB = ∠HMB(c/m t)

              Chung cạnh BM

              ∠ABM = ∠HBM(gt)

⇒ΔBAM = ΔBHM(g-c-g)

⇒ BA = BH (2 cạnh tương ứng)

⇒ΔABH cân tại B(Định nghĩa Δ cân)

c)*Xét ΔBAM và Δ BMC có:

            ∠ABM = ∠HBM(gt)

              Chung cạnh BM

              AB < BC( vì 3 cm < 5cm)

⇒  ΔBAM < ΔBMC(qh giữa góc và cạnh của Δ)

⇒ AM < MC(2 cạnh t/ứng)

d)*Xét ΔAKM và ΔMCK

Ta có: ∠KAM = ∠MHC(=90độ vì MH ⊥ BC ; ΔABC vg tại A)

            AM = AH(2 cạnh t/ứng do ΔBAM = ΔBHM)

            ∠AMK = ∠HMC( 2 góc đối đỉnh)

⇒ΔAKM = ΔMCK(g-c-g)

⇒MK = MC(2 cạnh t/ứng)

⇒ΔMKC cân tại M(đ/n Δ cân)

a) *Xét ΔABC vuông tại A có : AB² + AC² = BC²(Định lý Pytago)

Mà AB = 3cm ; BC=5cm(gt)

⇒      3² + AC² = 5²

⇒    9   +  AC² = 25

⇒             AC² = 25 - 9 = 16

⇒               AC = 4

Vậy cạnh AC = 4cm

b)*Xét ΔBAM vuông tại A có : ∠ABM + ∠AMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

*Xét ΔBHM vuông tại H có : ∠HBM + ∠HMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

⇒ ∠ABM + ∠AMB = ∠HBM + ∠HMB

Mà ∠ABM = ∠HBM( tia pg góc B cắt AC tại M)

⇒  ∠AMB = ∠HMB

*Xét ΔBAM và ΔBHM

Ta có : ∠AMB = ∠HMB(c/m t)

              Chung cạnh BM

              ∠ABM = ∠HBM(gt)

⇒ΔBAM = ΔBHM(g-c-g)

⇒ BA = BH (2 cạnh tương ứng)

⇒ΔABH cân tại B(Định nghĩa Δ cân)

c)*Xét ΔBAM và Δ BMC có:

            ∠ABM = ∠HBM(gt)

              Chung cạnh BM

              AB < BC( vì 3 cm < 5cm)

⇒  ΔBAM < ΔBMC(qh giữa góc và cạnh của Δ)

⇒ AM < MC(2 cạnh t/ứng)

d)*Xét ΔAKM và ΔMCK

Ta có: ∠KAM = ∠MHC(=90độ vì MH ⊥ BC ; ΔABC vg tại A)

            AM = AH(2 cạnh t/ứng do ΔBAM = ΔBHM)

            ∠AMK = ∠HMC( 2 góc đối đỉnh)

⇒ΔAKM = ΔMCK(g-c-g)

⇒MK = MC(2 cạnh t/ứng)

⇒ΔMKC cân tại M(đ/n Δ cân)

a) *Xét ΔABC vuông tại A có : AB² + AC² = BC²(Định lý Pytago)

Mà AB = 3cm ; BC=5cm(gt)

⇒      3² + AC² = 5²

⇒    9   +  AC² = 25

⇒             AC² = 25 - 9 = 16

⇒               AC = 4

Vậy cạnh AC = 4cm

b)*Xét ΔBAM vuông tại A có : ∠ABM + ∠AMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

*Xét ΔBHM vuông tại H có : ∠HBM + ∠HMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

⇒ ∠ABM + ∠AMB = ∠HBM + ∠HMB

Mà ∠ABM = ∠HBM( tia pg góc B cắt AC tại M)

⇒  ∠AMB = ∠HMB

*Xét ΔBAM và ΔBHM

Ta có : ∠AMB = ∠HMB(c/m t)

              Chung cạnh BM

              ∠ABM = ∠HBM(gt)

⇒ΔBAM = ΔBHM(g-c-g)

⇒ BA = BH (2 cạnh tương ứng)

⇒ΔABH cân tại B(Định nghĩa Δ cân)

c)*Xét ΔBAM và Δ BMC có:

            ∠ABM = ∠HBM(gt)

              Chung cạnh BM

              AB < BC( vì 3 cm < 5cm)

⇒  ΔBAM < ΔBMC(qh giữa góc và cạnh của Δ)

⇒ AM < MC(2 cạnh t/ứng)

d)*Xét ΔAKM và ΔMCK

Ta có: ∠KAM = ∠MHC(=90độ vì MH ⊥ BC ; ΔABC vg tại A)

            AM = AH(2 cạnh t/ứng do ΔBAM = ΔBHM)

            ∠AMK = ∠HMC( 2 góc đối đỉnh)

⇒ΔAKM = ΔMCK(g-c-g)

⇒MK = MC(2 cạnh t/ứng)

⇒ΔMKC cân tại M(đ/n Δ cân)

Câu e bn thông cảm cho mk nhé

a) *Xét ΔABC vuông tại A có : AB² + AC² = BC²(Định lý Pytago)

Mà AB = 3cm ; BC=5cm(gt)

⇒      3² + AC² = 5²

⇒    9   +  AC² = 25

⇒             AC² = 25 - 9 = 16

⇒               AC = 4

Vậy cạnh AC = 4cm

b)*Xét ΔBAM vuông tại A có : ∠ABM + ∠AMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

*Xét ΔBHM vuông tại H có : ∠HBM + ∠HMB = 90 độ (đ/lý tổng 2 góc nhọn phụ nhau trong Δ vg)

⇒ ∠ABM + ∠AMB = ∠HBM + ∠HMB

Mà ∠ABM = ∠HBM( tia pg góc B cắt AC tại M)

⇒  ∠AMB = ∠HMB

*Xét ΔBAM và ΔBHM

Ta có : ∠AMB = ∠HMB(c/m t)

              Chung cạnh BM

              ∠ABM = ∠HBM(gt)

⇒ΔBAM = ΔBHM(g-c-g)

⇒ BA = BH (2 cạnh tương ứng)

⇒ΔABH cân tại B(Định nghĩa Δ cân)

c)*Xét ΔBAM và Δ BMC có:

            ∠ABM = ∠HBM(gt)

              Chung cạnh BM

              AB < BC( vì 3 cm < 5cm)

⇒  ΔBAM < ΔBMC(qh giữa góc và cạnh của Δ)

⇒ AM < MC(2 cạnh t/ứng)

d)*Xét ΔAKM và ΔMCK

Ta có: ∠KAM = ∠MHC(=90độ vì MH ⊥ BC ; ΔABC vg tại A)

            AM = AH(2 cạnh t/ứng do ΔBAM = ΔBHM)

            ∠AMK = ∠HMC( 2 góc đối đỉnh)

⇒ΔAKM = ΔMCK(g-c-g)

⇒MK = MC(2 cạnh t/ứng)

⇒ΔMKC cân tại M(đ/n Δ cân)

Câu e bn thông cảm cho mk nhé