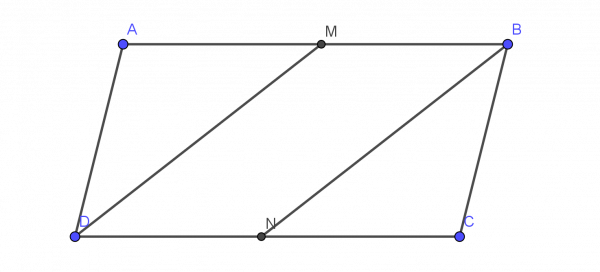
cho hình bình hành ABCD , đường phân giác của góc D cắt AB tại M , phân giác của B cắt CD tại N . Chứng minh rằng :
a) AM=CN
b) DMBN là hình bình hành
Quảng cáo
1 câu trả lời 6859
a) Ta có tứ giác ABCD là hbh
=> AD=BC và Góc DAB=Góc BCD; Góc ADC=Góc ABC
Mà DM và BN lần lượt là tia phân giác của góc ADC và góc ABC
=>Góc ADM=Góc CBN
Xét tam giác ADM và tam giác CBN có:
Góc ADM=Góc CBN
AD=BC
Góc DAM=Góc BCN
=> Tam giác ADM=tam giác CBN
=> AM=CN
b) Do tứ giác ABCD là hbh nên AB=CD và AB//CD
Có AM=CN=> AB-AM=CD-CN
=> BM=DN
Xét tứ giác BMDN có BM//DN
BM=DN
=>Tứ giác BMDN là hbh
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


