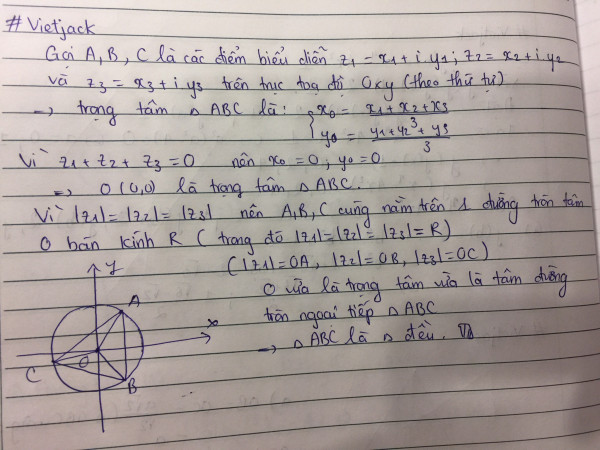Chứng minh rằng: là ba số phức phân biệt thỏa mãn và thì 3 điểm là 3 đỉnh của 1 tam giác đều.
Quảng cáo
1 câu trả lời 3399
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340
Gửi báo cáo thành công!