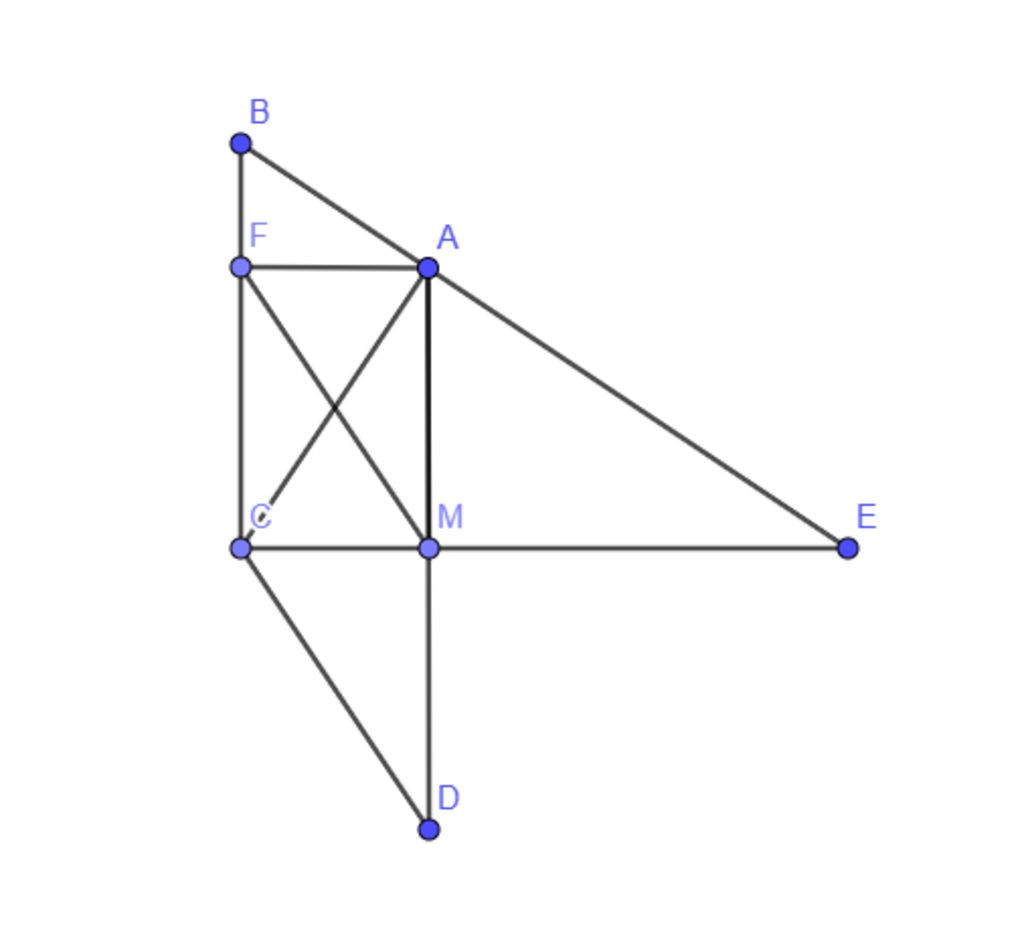
Cho tam giác CBE vuông tại C (CB < EC) có CA là đường cao. Kẻ AF vuông góc CB tại F, kẻ AM vuông góc E tại M. a) Chứng minh tứ giác AMCF là hình chữ nhật. b) Lấy điểm D đối xứng với điểm A qua điểm M. Chứng minh tứ giác CDMF là hình bình hành.
Quảng cáo
1 câu trả lời 121
`a)`
Xét tứ giác `AMCF` có: `\hat{AFC}=\hat{FCM}=\hat{AMC}=90^@`
`=> AMCF ` là hình chữ nhật
`b)`
Có `D` đối xứng với `A` qua `M`
`=> MD=MA`
Vì `AMCF` là hình chữ nhật
`=> MA=CF; MA//CF`
mà `DinMA => MD//CF`
mà `MD=MA => MD=CF`
`=> CDMF` là hình bình hành
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191
Gửi báo cáo thành công!


