Đề bài tóm tắt
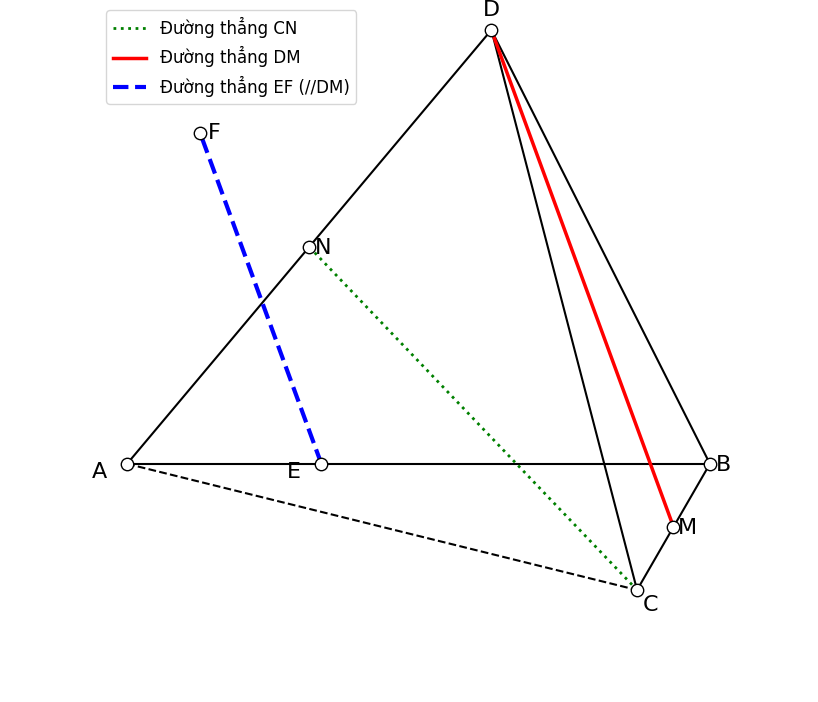
Tứ diện ABCDABCDABCD có các cạnh bằng 1

MMM là trung điểm của BCBCBC
NNN là trung điểm của ADADAD
Trên đường thẳng ABABAB lấy điểm EEE.
Trên đường thẳng CNCNCN lấy điểm FFF.
Sao cho EF∥DMEF \parallel DMEF∥DM.
Tính độ dài EFEFEF.

Bước 1. Chọn hệ tọa độ thuận lợi
Đặt tứ diện đều ABCDABCDABCD cạnh 111 vào hệ tọa độ:

{A(0,0,0)B(1,0,0)C(12,32,0)D(12,36,63)\begin{cases} A(0,0,0) \\ B(1,0,0) \\ C\left(\frac{1}{2}, \frac{\sqrt{3}}{2}, 0\right) \\ D\left(\frac{1}{2}, \frac{\sqrt{3}}{6}, \frac{\sqrt{6}}{3}\right) \end{cases}⎩⎨⎧​A(0,0,0)B(1,0,0)C(21​,23​​,0)D(21​,63​​,36​​)​
Bước 2. Xác định các điểm trung điểm
M=Trung điểm của BC⇒M(1+122,0+322,0)=(34,34,0)M = \text{Trung điểm của } BC \Rightarrow M\left( \frac{1+ \frac{1}{2}}{2}, \frac{0 + \frac{\sqrt{3}}{2}}{2}, 0 \right) = \left(\frac{3}{4}, \frac{\sqrt{3}}{4}, 0\right)M=Trung điểm của BC⇒M(21+21​​,20+23​​​,0)=(43​,43​​,0) N=Trung điểm của AD⇒N(0+122,0+362,0+632)=(14,312,66)N = \text{Trung điểm của } AD \Rightarrow N\left( \frac{0 + \frac{1}{2}}{2}, \frac{0 + \frac{\sqrt{3}}{6}}{2}, \frac{0 + \frac{\sqrt{6}}{3}}{2} \right) = \left(\frac{1}{4}, \frac{\sqrt{3}}{12}, \frac{\sqrt{6}}{6}\right)N=Trung điểm của AD⇒N(20+21​​,20+63​​​,20+36​​​)=(41​,123​​,66​​)
Bước 3. Biểu diễn các đường thẳng
Đường ABABAB:

A(0,0,0),  B(1,0,0)⇒phương trıˋnh: (x,y,z)=(t,0,0)A(0,0,0),\; B(1,0,0) \Rightarrow \text{phương trình: } (x, y, z) = (t, 0, 0)A(0,0,0),B(1,0,0)⇒phương trıˋnh: (x,y,z)=(t,0,0)→ E(t,0,0)E(t, 0, 0)E(t,0,0), với t∈Rt \in \mathbb{R}t∈R.
Đường CNCNCN:

C(12,32,0),  N(14,312,66)C\left(\frac{1}{2}, \frac{\sqrt{3}}{2}, 0\right),\; N\left(\frac{1}{4}, \frac{\sqrt{3}}{12}, \frac{\sqrt{6}}{6}\right)C(21​,23​​,0),N(41​,123​​,66​​)→ VTPT của CNCNCN:

vCN⃗=N−C=(−14,−5312,66)\vec{v_{CN}} = N - C = \left(-\frac{1}{4}, -\frac{5\sqrt{3}}{12}, \frac{\sqrt{6}}{6}\right)vCN​​=N−C=(−41​,−1253​​,66​​)→ Điểm FFF trên CNCNCN:

F=C+svCN⃗=(12−s4,32−5s312,s66)F = C + s\vec{v_{CN}} = \left(\frac{1}{2} - \frac{s}{4}, \frac{\sqrt{3}}{2} - \frac{5s\sqrt{3}}{12}, \frac{s\sqrt{6}}{6}\right)F=C+svCN​​=(21​−4s​,23​​−125s3​​,6s6​​)

Bước 4. Tính vectơ DM→\overrightarrow{DM}DM
DM⃗=M−D=(34−12,34−36,0−63)=(14,312,−63)\vec{DM} = M - D = \left(\frac{3}{4} - \frac{1}{2}, \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{6}, 0 - \frac{\sqrt{6}}{3}\right) = \left(\frac{1}{4}, \frac{\sqrt{3}}{12}, -\frac{\sqrt{6}}{3}\right)DM=M−D=(43​−21​,43​​−63​​,0−36​​)=(41​,123​​,−36​​)
Bước 5. Điều kiện song song EF∥DMEF \parallel DMEF∥DM
EF⃗=FE→=E−F\vec{EF} = \overrightarrow{F E} = E - FEF=FE=E−FTừ tọa độ:

EF⃗=(t−(12−s4),0−(32−5s312),0−s66)\vec{EF} = \left(t - \left(\frac{1}{2} - \frac{s}{4}\right), 0 - \left(\frac{\sqrt{3}}{2} - \frac{5s\sqrt{3}}{12}\right), 0 - \frac{s\sqrt{6}}{6}\right)EF=(t−(21​−4s​),0−(23​​−125s3​​),0−6s6​​) =(t−12+s4,−32+5s312,−s66)= \left(t - \frac{1}{2} + \frac{s}{4}, -\frac{\sqrt{3}}{2} + \frac{5s\sqrt{3}}{12}, -\frac{s\sqrt{6}}{6}\right)=(t−21​+4s​,−23​​+125s3​​,−6s6​​)Điều kiện:

EF⃗=kDM⃗\vec{EF} = k \vec{DM}EF=kDM
Bước 6. Lập hệ tỉ số theo từng tọa độ
t−12+s414=−32+5s312312=−s66−63=k\frac{t - \frac{1}{2} + \frac{s}{4}}{\frac{1}{4}} = \frac{-\frac{\sqrt{3}}{2} + \frac{5s\sqrt{3}}{12}}{\frac{\sqrt{3}}{12}} = \frac{-\frac{s\sqrt{6}}{6}}{-\frac{\sqrt{6}}{3}} = k41​t−21​+4s​​=123​​−23​​+125s3​​​=−36​​−6s6​​​=kTừ trục zzz:

s/61/3=s2⇒k=s2\frac{s/6}{1/3} = \frac{s}{2} \Rightarrow k = \frac{s}{2}1/3s/6​=2s​⇒k=2s​Thay vào trục xxx:

t−12+s4=14⋅s2=s8t - \frac{1}{2} + \frac{s}{4} = \frac{1}{4} \cdot \frac{s}{2} = \frac{s}{8}t−21​+4s​=41​⋅2s​=8s​ ⇒t=12−s4+s8=12−s8\Rightarrow t = \frac{1}{2} - \frac{s}{4} + \frac{s}{8} = \frac{1}{2} - \frac{s}{8}⇒t=21​−4s​+8s​=21​−8s​Kiểm tra trục yyy:

−12+5s12=112⋅s2=s24-\frac{1}{2} + \frac{5s}{12} = \frac{1}{12} \cdot \frac{s}{2} = \frac{s}{24}−21​+125s​=121​⋅2s​=24s​Nhân 24 hai vế:

−12+10s=s⇒9s=12⇒s=43-12 + 10s = s \Rightarrow 9s = 12 \Rightarrow s = \frac{4}{3}−12+10s=s⇒9s=12⇒s=34​Thay vào t=12−s8=12−16=13t = \frac{1}{2} - \frac{s}{8} = \frac{1}{2} - \frac{1}{6} = \frac{1}{3}t=21​−8s​=21​−61​=31​

Bước 7. Xác định tọa độ E, F
E(13,0,0)E\left(\frac{1}{3}, 0, 0\right)E(31​,0,0) F=(12−13⋅14,32−5312⋅43,66⋅43)⇒F(16,36,269)F = \left(\frac{1}{2} - \frac{1}{3}\cdot\frac{1}{4}, \frac{\sqrt{3}}{2} - \frac{5\sqrt{3}}{12}\cdot\frac{4}{3}, \frac{\sqrt{6}}{6}\cdot\frac{4}{3}\right) \Rightarrow F\left(\frac{1}{6}, \frac{\sqrt{3}}{6}, \frac{2\sqrt{6}}{9}\right)F=(21​−31​⋅41​,23​​−1253​​⋅34​,66​​⋅34​)⇒F(61​,63​​,926​​)
Bước 8. Tính độ dài EFEFEF
EF2=(13−16)2+(0−36)2+(0−269)2EF^2 = \left(\frac{1}{3} - \frac{1}{6}\right)^2 + \left(0 - \frac{\sqrt{3}}{6}\right)^2 + \left(0 - \frac{2\sqrt{6}}{9}\right)^2EF2=(31​−61​)2+(0−63​​)2+(0−926​​)2 =(16)2+(36)2+(269)2=136+336+2481= \left(\frac{1}{6}\right)^2 + \left(\frac{\sqrt{3}}{6}\right)^2 + \left(\frac{2\sqrt{6}}{9}\right)^2 = \frac{1}{36} + \frac{3}{36} + \frac{24}{81}=(61​)2+(63​​)2+(926​​)2=361​+363​+8124​ =436+827=19+827=3+827=1127= \frac{4}{36} + \frac{8}{27} = \frac{1}{9} + \frac{8}{27} = \frac{3 + 8}{27} = \frac{11}{27}=364​+278​=91​+278​=273+8​=2711​ ⇒EF=1127=339\Rightarrow EF = \sqrt{\frac{11}{27}} = \frac{\sqrt{33}}{9}⇒EF=2711​​=933​​
✅ Kết luận:

EF=339\boxed{EF = \dfrac{\sqrt{33}}{9}}EF=933​​​
 
 

Bước 1: Chọn hệ tọa độ
Để tính toán dễ, đặt tứ diện ABCDABCDABCD sao cho:

A=(0,0,0),B=(1,0,0),C=(0,1,0),D=(0,0,1)A=(0,0,0), \quad B=(1,0,0), \quad C=(0,1,0), \quad D=(0,0,1)A=(0,0,0),B=(1,0,0),C=(0,1,0),D=(0,0,1)Vì tất cả cạnh = 1, đây là tứ diện đều.

Bước 2: Xác định các điểm M, N, D, C
MMM là trung điểm BCBCBC:
B=(1,0,0),C=(0,1,0)  ⟹  M=(1+02,0+12,0+02)=(12,12,0)B=(1,0,0), C=(0,1,0) \implies M = \left(\frac{1+0}{2}, \frac{0+1}{2}, \frac{0+0}{2}\right) = \left(\frac{1}{2}, \frac{1}{2}, 0\right)B=(1,0,0),C=(0,1,0)⟹M=(21+0​,20+1​,20+0​)=(21​,21​,0)NNN là trung điểm ADADAD:
A=(0,0,0),D=(0,0,1)  ⟹  N=(0,0,12)A=(0,0,0), D=(0,0,1) \implies N = \left(0,0,\frac{1}{2}\right)A=(0,0,0),D=(0,0,1)⟹N=(0,0,21​)D=(0,0,1)D=(0,0,1)D=(0,0,1) (có sẵn)

Bước 3: Xác định tham số cho E và F
EEE trên ABABAB:
AB:x=t,y=0,z=0,t∈[0,1]  ⟹  E=(t,0,0)AB: x=t, y=0, z=0, \quad t \in [0,1] \implies E=(t,0,0)AB:x=t,y=0,z=0,t∈[0,1]⟹E=(t,0,0)FFF trên CNCNCN:
C=(0,1,0),N=(0,0,1)  ⟹  CN:r=C+s(N−C)=(0,1,0)+s(0,−1,1)=(0,1−s,s),s∈[0,1]C=(0,1,0), N=(0,0,1) \implies CN: \mathbf{r} = C + s(N-C) = (0,1,0) + s(0,-1,1) = (0,1-s,s), \quad s\in[0,1]C=(0,1,0),N=(0,0,1)⟹CN:r=C+s(N−C)=(0,1,0)+s(0,−1,1)=(0,1−s,s),s∈[0,1]Vậy F=(0,1−s,s)F = (0, 1-s, s)F=(0,1−s,s).

Bước 4: Điều kiện EF∥DMEF \parallel DMEF∥DM
D=(0,0,1),M=(1/2,1/2,0)D=(0,0,1), M=(1/2, 1/2,0)D=(0,0,1),M=(1/2,1/2,0)
DM⃗=M−D=(12−0,12−0,0−1)=(12,12,−1)\vec{DM} = M-D = \left(\frac{1}{2}-0, \frac{1}{2}-0, 0-1\right) = \left(\frac{1}{2}, \frac{1}{2}, -1\right)DM=M−D=(21​−0,21​−0,0−1)=(21​,21​,−1)EF⃗=F−E=(0−t,(1−s)−0,s−0)=(−t,1−s,s)\vec{EF} = F-E = (0-t, (1-s)-0, s-0) = (-t, 1-s, s)EF=F−E=(0−t,(1−s)−0,s−0)=(−t,1−s,s)
EF // DM → EF⃗=kDM⃗\vec{EF} = k \vec{DM}EF=kDM với một số thực kkk
(−t,1−s,s)=k(12,12,−1)(-t, 1-s, s) = k\left(\frac{1}{2}, \frac{1}{2}, -1\right)(−t,1−s,s)=k(21​,21​,−1)
Bước 5: Giải hệ phương trình
Từ đó ta có:

−t=k2  ⟹  k=−2t-t = \frac{k}{2} \implies k = -2t−t=2k​⟹k=−2t
1−s=k2=−t  ⟹  s=1+t1-s = \frac{k}{2} = -t \implies s = 1 + t1−s=2k​=−t⟹s=1+t
s=−k=2ts = -k = 2ts=−k=2t
So sánh 2 biểu thức của sss:

2t=1+t  ⟹  t=12t = 1 + t \implies t = 12t=1+t⟹t=1Vậy t=1  ⟹  E=(1,0,0)t=1 \implies E = (1,0,0)t=1⟹E=(1,0,0)

s=2t=2  ⟹  F=(0,1−s,s)=(0,1−2,2)=(0,−1,2)s = 2t = 2 \implies F=(0,1-s,s) = (0,1-2,2) = (0,-1,2)s=2t=2⟹F=(0,1−s,s)=(0,1−2,2)=(0,−1,2)
Bước 6: Tính EF
E=(1,0,0),F=(0,−1,2)E=(1,0,0), F=(0,-1,2)E=(1,0,0),F=(0,−1,2) EF=(1−0)2+(0−(−1))2+(0−2)2=12+12+(−2)2=1+1+4=6EF = \sqrt{(1-0)^2 + (0-(-1))^2 + (0-2)^2} = \sqrt{1^2 + 1^2 + (-2)^2} = \sqrt{1+1+4} = \sqrt{6}EF=(1−0)2+(0−(−1))2+(0−2)2​=12+12+(−2)2​=1+1+4​=6​
✅ Kết luận
EF=6\boxed{EF = \sqrt{6}}EF=6​​

$\displaystyle \text{Chọn hệ trục tọa độ Oxyz sao cho } A(0,0,0), B(1,0,0), C(\frac{1}{2}, \frac{\sqrt{3}}{2}, 0), D(\frac{1}{2}, \frac{\sqrt{3}}{6}, \frac{\sqrt{6}}{3}).$

$\displaystyle M \text{ là trung điểm } BC \implies M(\frac{3}{4}, \frac{\sqrt{3}}{4}, 0).$
$\displaystyle N \text{ là trung điểm } AD \implies N(\frac{1}{4}, \frac{\sqrt{3}}{12}, \frac{\sqrt{6}}{6}).$

$\displaystyle \vec{DM} = (\frac{1}{4}, \frac{\sqrt{3}}{12}, -\frac{\sqrt{6}}{3}).$
$\displaystyle \vec{CN} = (-\frac{1}{4}, -\frac{5\sqrt{3}}{12}, \frac{\sqrt{6}}{6}).$

$\displaystyle E \in AB \implies E(t, 0, 0).$
$\displaystyle F \in CN \implies \vec{F} = \vec{C} + u\vec{CN} = (\frac{1}{2}-\frac{u}{4}, \frac{\sqrt{3}}{2}-\frac{5\sqrt{3}u}{12}, \frac{\sqrt{6}u}{6}).$

$\displaystyle \vec{EF} = (\frac{1}{2}-\frac{u}{4}-t, \frac{\sqrt{3}}{2}-\frac{5\sqrt{3}u}{12}, \frac{\sqrt{6}u}{6}).$

$\displaystyle \text{Do } EF // DM \implies \vec{EF} = k\vec{DM}.$
$\displaystyle \implies \begin{cases} \frac{1}{2}-\frac{u}{4}-t = \frac{k}{4} \\ \frac{\sqrt{3}}{2}-\frac{5\sqrt{3}u}{12} = k \frac{\sqrt{3}}{12} \implies 6-5u=k \\ \frac{\sqrt{6}u}{6} = -k \frac{\sqrt{6}}{3} \implies u=-2k \end{cases}$

$\displaystyle \text{Thay } u=-2k \text{ vào } 6-5u=k \implies 6-5(-2k)=k \implies 6+10k=k \implies 9k=-6 \implies k=-\frac{2}{3}.$

$\displaystyle |\vec{DM}| = \sqrt{(\frac{1}{4})^2 + (\frac{\sqrt{3}}{12})^2 + (-\frac{\sqrt{6}}{3})^2} = \sqrt{\frac{1}{16} + \frac{3}{144} + \frac{6}{9}} = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}.$

$\displaystyle EF = |k| \cdot |\vec{DM}| = |-\frac{2}{3}| \cdot \frac{\sqrt{3}}{2} = \frac{2}{3} \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{3}.$

$\displaystyle \text{Vậy, } EF = \frac{\sqrt{3}}{3}.$

Bài toán này yêu cầu tính độ dài đoạn thẳng $EF$ biết $EF \parallel DM$.

📐 Phân tích hình học và Xác định tỉ lệ
Tứ diện $ABCD$ có tất cả các cạnh bằng $1$ là một tứ diện đều.

Xác định vị trí các điểm:

$M$ là trung điểm của $BC$.
$N$ là trung điểm của $AD$.
$E$ nằm trên đường thẳng $AB$.
$F$ nằm trên đường thẳng $CN$.
$EF \parallel DM$.
Sử dụng tính chất song song:

Vì $EF \parallel DM$, ba điểm $E, F, M$ đồng phẳng và $E, F, D$ đồng phẳng.

Xét mặt phẳng chứa $DM$ và đường thẳng $CN$.

Do $EF \parallel DM$, ta có thể áp dụng định lí Ta-lét (Talos) hoặc phương pháp vector.

$E$ nằm trên $AB$ và $F$ nằm trên $CN$.
Gọi $G$ là giao điểm của $EF$ và mặt phẳng $(CDM)$. Do $EF \parallel DM$, thì $EF$ phải nằm trong mặt phẳng $(CDM)$ hoặc song song với nó.
Tuy nhiên, $E \in AB$ và $F \in CN$. Ta sẽ dùng phương pháp vector để giải.
✍️ Giải bằng phương pháp Vector
Chọn $\vec{A}$ là gốc toạ độ. Đặt $\vec{u} = \vec{AB}$, $\vec{v} = \vec{AC}$, $\vec{w} = \vec{AD}$.

Vì $ABCD$ là tứ diện đều có cạnh bằng $1$, ta có:

$|\vec{u}| = |\vec{v}| = |\vec{w}| = 1$
$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$
Biểu diễn các vector $\vec{DM}$ và $\vec{EF}$:

Vector $\vec{DM}$:

$\vec{DM} = \vec{AM} - \vec{AD} = \frac{\vec{AB} + \vec{AC}}{2} - \vec{AD} = \frac{1}{2}\vec{u} + \frac{1}{2}\vec{v} - \vec{w}$
Vector $\vec{EF}$:

Vì $E \in AB$, đặt $\vec{AE} = k \cdot \vec{AB} = k \vec{u}$.

Vì $F \in CN$, đặt $\vec{NF} = l \cdot \vec{NC}$, hay $\vec{AF} = (1-t) \vec{AN} + t \vec{AC}$, với $t \in \mathbb{R}$.

Vì $N$ là trung điểm của $AD$, $\vec{AN} = \frac{1}{2}\vec{AD} = \frac{1}{2}\vec{w}$.

$\vec{AF} = (1-t) \frac{1}{2}\vec{w} + t \vec{v} = t\vec{v} + \frac{1-t}{2}\vec{w}$
$\vec{EF} = \vec{AF} - \vec{AE} = t\vec{v} + \frac{1-t}{2}\vec{w} - k\vec{u} = -k\vec{u} + t\vec{v} + \frac{1-t}{2}\vec{w}$
Áp dụng điều kiện song song $\vec{EF} \parallel \vec{DM}$:

Tồn tại số thực $\lambda$ sao cho $\vec{EF} = \lambda \vec{DM}$.

$-k\vec{u} + t\vec{v} + \frac{1-t}{2}\vec{w} = \lambda \left( \frac{1}{2}\vec{u} + \frac{1}{2}\vec{v} - \vec{w} \right)$
$-k\vec{u} + t\vec{v} + \frac{1-t}{2}\vec{w} = \frac{\lambda}{2}\vec{u} + \frac{\lambda}{2}\vec{v} - \lambda\vec{w}$
Vì $\vec{u}, \vec{v}, \vec{w}$ không đồng phẳng, ta có thể so sánh các hệ số:

(hệ số $\vec{u}$): $-k = \frac{\lambda}{2} \implies \lambda = -2k$
(hệ số $\vec{v}$): $t = \frac{\lambda}{2} \implies \lambda = 2t$
(hệ số $\vec{w}$): $\frac{1-t}{2} = -\lambda \implies 1-t = -2\lambda$
Giải hệ phương trình tìm $t, k, \lambda$:

Từ hai phương trình đầu: $-2k = 2t \implies \mathbf{k = -t}$

Thay $\lambda = 2t$ vào phương trình thứ ba:

$1 - t = -2(2t) \implies 1 - t = -4t$
$3t = -1 \implies t = -\frac{1}{3}$
Từ đó, ta tìm được:

$k = -t = -(-\frac{1}{3}) = \frac{1}{3}$
$\lambda = 2t = 2(-\frac{1}{3}) = -\frac{2}{3}$
Tính độ dài $EF$:

Ta có $\vec{EF} = \lambda \vec{DM}$.

$|\vec{EF}| = |\lambda| \cdot |\vec{DM}| = \left|-\frac{2}{3}\right| \cdot |\vec{DM}| = \frac{2}{3} |\vec{DM}|$
Tính $|\vec{DM}|^2$:

$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$0
$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$1
 

Thay $|\vec{u}|^2 = |\vec{v}|^2 = |\vec{w}|^2 = 1$ và $\vec{u}\cdot\vec{v} = \vec{v}\cdot\vec{w} = \vec{w}\cdot\vec{u} = \frac{1}{2}$:

$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$2
$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$3
$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$4
$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$5
Tính độ dài $EF$:

$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 1 \cdot 1 \cdot \cos(60^\circ) = \frac{1}{2}$6

✅ Kết quả
Độ dài đoạn thẳng $EF$ là $\frac{\sqrt{3}}{3}$.