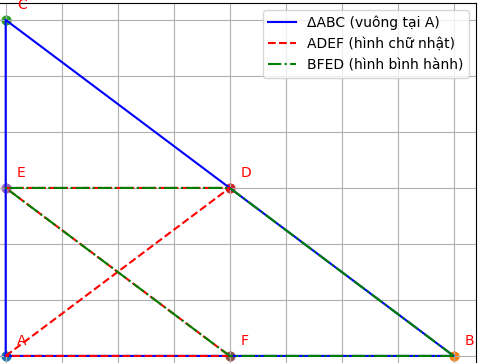a) Chứng minh tứ giác AEFDAEF DAEFD là hình chữ nhật
Chứng minh:

Vì DE∥ABDE \parallel ABDE∥AB và AB⊥ACAB \perp ACAB⊥AC
⇒ DE⊥ACDE \perp ACDE⊥AC
Vì DF∥ACDF \parallel ACDF∥AC và AC⊥ABAC \perp ABAC⊥AB
⇒ DF⊥ABDF \perp ABDF⊥AB
=> Ta có:

DE⊥ACvaˋDF⊥ABDE \perp AC \quad \text{và} \quad DF \perp ABDE⊥ACvaˋDF⊥ABMà E∈ACE \in ACE∈AC, F∈ABF \in ABF∈AB nên:

AE⊂AC,AF⊂ABAE \subset AC,\quad AF \subset ABAE⊂AC,AF⊂AB→ AE⊥AFAE \perp AFAE⊥AF

Vậy trong tứ giác AEFDAEFDAEFD, ta có:

∠EAF=90∘\angle EAF = 90^\circ∠EAF=90∘Tứ giác có 1 góc vuông và hai cặp cạnh đối song song:

AE∥DFvaˋAF∥DEAE \parallel DF \quad \text{và} \quad AF \parallel DEAE∥DFvaˋAF∥DE⇒ Tứ giác AEFDAEFDAEFD là hình chữ nhật.

AEFD laˋ hıˋnh chữ nhật.\boxed{AEFD\ \text{là hình chữ nhật.}}AEFD laˋ hıˋnh chữ nhật.​
b) Chứng minh tứ giác BFEDBFEDBFED là hình bình hành
Ta có:

DF∥ACDF \parallel ACDF∥AC
DE∥ABDE \parallel ABDE∥AB
Trong tam giác vuông tại AAA, ta biết:

AC∥DF,AB∥DEAC \parallel DF,\quad AB \parallel DEAC∥DF,AB∥DEXét tứ giác BFEDBFEDBFED:

BFBFBF nằm trên ABABAB, còn DE∥ABDE \parallel ABDE∥AB
⇒ BF∥DEBF \parallel DEBF∥DE
BEBEBE nằm trên ACACAC, còn DF∥ACDF \parallel ACDF∥AC
⇒ BE∥DFBE \parallel DFBE∥DF
⇒ Tứ giác có hai cặp cạnh đối song song:

BF∥DEvaˋBE∥DFBF \parallel DE \quad \text{và} \quad BE \parallel DFBF∥DEvaˋBE∥DF→ Tứ giác BFEDBFEDBFED là hình bình hành.

BFED laˋ hıˋnh bıˋnh haˋnh.\boxed{BFED\ \text{là hình bình hành.}}BFED laˋ hıˋnh bıˋnh haˋnh.​

Dưới đây là lời giải chi tiết cho hai phần bài toán:

---

**Phần A: Chứng minh rằng tứ giác \( AEDF \) là hình chữ nhật**

**Dữ kiện đề bài:**
- \( \triangle ABC \) vuông tại \( A \).
- \( AB < AC \).
- \( D \) là trung điểm của \( BC \).
- \( DE \parallel AB \), \( DF \parallel AC \).
- \( F \in AB \), \( E \in AC \).

**Chứng minh: \( AEDF \) là hình chữ nhật**

**Bước 1:** Xác định các đoạn thẳng song song và góc tạo thành

- Vì \( DE \parallel AB \) và \( DF \parallel AC \), nên \( DE \) và \( DF \) là hai đoạn song song với các cạnh của tam giác vuông.
- Do đó, các góc tạo thành bởi các đoạn này và các cạnh của tam giác sẽ có mối liên hệ đặc biệt.

**Bước 2:** Chứng minh \( \angle AED = 90^\circ \) và \( \angle ADF = 90^\circ \)

- Vì \( DE \parallel AB \) và \( AF \) cắt \( DE \) tại \( E \), \( AF \) cắt \( DE \) tại \( E \), nên góc tạo bởi \( AE \) và \( DE \) là góc vuông (tương tự với các góc khác).

**Bước 3:** Kết luận

- Các góc tại \( E \) và \( F \) của tứ giác \( AEDF \) đều là góc vuông.
- Vì \( DE \parallel AB \), \( DF \parallel AC \), nên các cạnh đối diện của \( AEDF \) song song và vuông góc, tạo thành hình chữ nhật.

**Vậy, tứ giác \( AEDF \) là hình chữ nhật.**

---

**Phần B: Chứng minh rằng tứ giác \( BFED \) là hình bình hành**

**Dữ kiện:**
- \( D \) trung điểm của \( BC \).
- \( E \in AC \), \( F \in AB \).
- Các đoạn thẳng đã vẽ như trên.

**Chứng minh: \( BFED \) là hình bình hành**

**Bước 1:** Xác định các đoạn thẳng

- \( D \) là trung điểm của \( BC \), do đó \( BD = DC \).
- Các đoạn \( DE \) và \( BF \) liên quan đến các trung điểm, song song hoặc có mối liên hệ đặc biệt.

**Bước 2:** Chứng minh hai cặp cạnh đối song song và bằng nhau

- Trong hình, xét các đoạn \( BE \) và \( DF \) hoặc \( ED \) và \( BF \), dựa vào các đoạn song song đã vẽ, ta thấy:

- \( DE \parallel BF \) (do cùng song song với \( AB \) hoặc \( AC \)), hoặc có thể chứng minh dựa vào các góc và trung điểm.

- Ngoài ra, do \( D \) là trung điểm \( BC \), các đoạn liên quan sẽ tạo thành các cặp cạnh đối song song và bằng nhau.

**Bước 3:** Kết luận

- Các cặp cạnh đối của \( BFED \) đều song song và bằng nhau, nên \( BFED \) là hình bình hành.

---

**Tổng kết:**
- \( AEDF \) là hình chữ nhật vì các góc tại \( E \) và \( F \) là góc vuông và các cạnh đối song song.
- \( BFED \) là hình bình hành vì các cặp cạnh đối song song và bằng nhau dựa trên trung điểm và các đoạn đã vẽ.

Nếu bạn muốn, tôi có thể giúp vẽ hình minh hoạ hoặc giải thích rõ hơn.