Y= (x² - 9x + 16) / (x - 4)
Hỏi tiệm cận xiên của đồ thị hàm số là đường thẳng y=?
Quảng cáo
2 câu trả lời 125
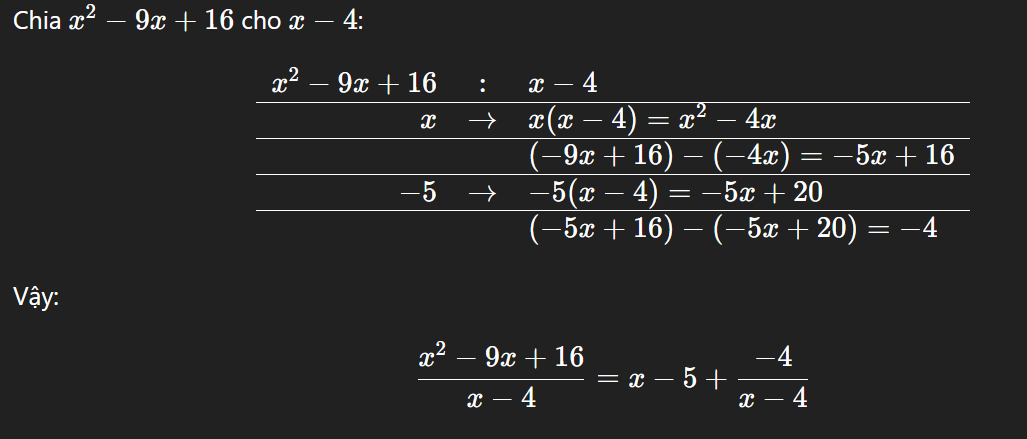
⟹ Tiệm cận xiên là đường thẳng: y = x − 5
Vậy: Đường tiệm cận xiên của đồ thị hàm số là: y = x − 5
Để tìm tiệm cận xiên của đồ thị hàm số \( y = \frac{x^2 - 9x + 16}{x - 4} \), chúng ta cần thực hiện phép chia đa thức để xem đồ thị có xu hướng gần đường thẳng nào khi \( x \to \pm \infty \).
---
**Bước 1:** Thực hiện phép chia đa thức
Chia \( x^2 - 9x + 16 \) cho \( x - 4 \):
Sử dụng phép chia đa thức:
- \( x^2 \div x = x \)
- Nhân \( x \) với \( x - 4 \): \( x(x - 4) = x^2 - 4x \)
- Trừ: \( (x^2 - 9x + 16) - (x^2 - 4x) = -5x + 16 \)
Tiếp tục chia:
- \( -5x \div x = -5 \)
- Nhân \( -5 \) với \( x - 4 \): \( -5(x - 4) = -5x + 20 \)
- Trừ: \( (-5x + 16) - (-5x + 20) = -4 \)
Vậy phép chia được:
\[
\frac{x^2 - 9x + 16}{x - 4} = x - 5 + \frac{-4}{x - 4}
\]
---
**Bước 2:** Xác định tiệm cận xiên
Khi \( x \to \pm \infty \), phần \( \frac{-4}{x - 4} \to 0 \), nên đồ thị hàm số tiệm cận theo đường thẳng:
\[
y = x - 5
\]
---
**Kết luận:**
**Đường thẳng tiệm cận xiên của đồ thị hàm số là:**
\[
\boxed{y = x - 5}
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



