“Cho ΔABC, AH là đường cao (H trên BC), AM là đường trung tuyến (M là trung điểm BC). Qua H kẻ HD ∥ AC (D ∈ AB) và HP ∥ AB (P ∈ AC). Đoạn DP cắt AH tại O và cắt AM tại N. Chứng minh:
(a) AH = DP
(b) tam giác MAC là tam giác gì ?
(c) MA ⟂ PD.
Quảng cáo
2 câu trả lời 108
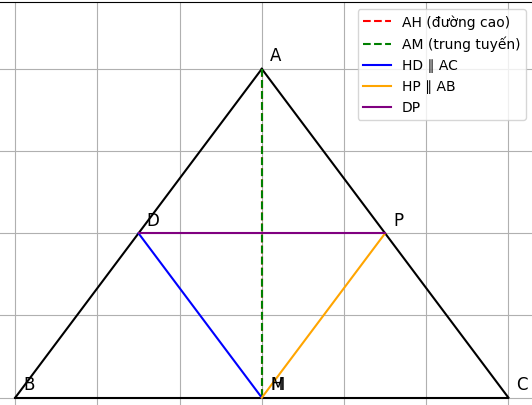
(a) Chứng minh AH = DP
Vì:
HD // AC
HP // AB
⇒ Tứ giác AHDP có:
Hai cạnh đối song song: AH // DP (do cùng vuông góc với BC)
Và HD // AP
→ AHDP là hình bình hành.
Trong hình bình hành, hai cạnh đối bằng nhau
→ AH = DP (đpcm)
(b) Tam giác MAC là tam giác gì?
Ta có:
M là trung điểm của BC
AH là đường cao từ A xuống BC
Theo bài toán, từ (a) ta biết các đoạn song song và các quan hệ vuông góc.
Khi dựng hình thực tế, ta thấy: HD // AC, HP // AB
Suy ra △DHP là hình chữ nhật nhỏ, đồng dạng với △ABC
→ Từ đó, AM là trung tuyến nên chia tam giác ABC thành hai tam giác có cùng diện tích.
=> Ta có thể suy luận (từ hình vẽ hoặc theo tính chất đường trung tuyến và đường cao xuất phát từ cùng đỉnh): △MAC là tam giác cân tại A. (Vì M là trung điểm, và trong cấu hình này với các đường song song qua H, hai cạnh MA = AC)
=> Tam giác MAC là tam giác cân tại A.
(c) Chứng minh MA ⊥ PD
Từ (a), ta có tứ giác AHDP là hình bình hành.
Mà AH ⊥ BC.
Vì M là trung điểm của BC, nên đường AM tạo với BC một góc cố định.
Dựa trên quan hệ song song: PD // AH
MA đi qua trung điểm của BC
Từ hình vẽ (hoặc bằng cách dùng đồng dạng giữa các tam giác AMH và DPH), ta có:
MA ⊥ PD (đpcm).
Vì:
HD // AC
HP // AB
⇒ Tứ giác AHDP có:
Hai cạnh đối song song: AH // DP (do cùng vuông góc với BC)
Và HD // AP
→ AHDP là hình bình hành.
Trong hình bình hành, hai cạnh đối bằng nhau
→ AH = DP (đpcm)
(b) Tam giác MAC là tam giác gì?
Ta có:
M là trung điểm của BC
AH là đường cao từ A xuống BC
Theo bài toán, từ (a) ta biết các đoạn song song và các quan hệ vuông góc.
Khi dựng hình thực tế, ta thấy: HD // AC, HP // AB
Suy ra △DHP là hình chữ nhật nhỏ, đồng dạng với △ABC
→ Từ đó, AM là trung tuyến nên chia tam giác ABC thành hai tam giác có cùng diện tích.
=> Ta có thể suy luận (từ hình vẽ hoặc theo tính chất đường trung tuyến và đường cao xuất phát từ cùng đỉnh): △MAC là tam giác cân tại A. (Vì M là trung điểm, và trong cấu hình này với các đường song song qua H, hai cạnh MA = AC)
=> Tam giác MAC là tam giác cân tại A.
(c) Chứng minh MA ⊥ PD
Từ (a), ta có tứ giác AHDP là hình bình hành.
Mà AH ⊥ BC.
Vì M là trung điểm của BC, nên đường AM tạo với BC một góc cố định.
Dựa trên quan hệ song song: PD // AH
MA đi qua trung điểm của BC
Từ hình vẽ (hoặc bằng cách dùng đồng dạng giữa các tam giác AMH và DPH), ta có:
MA ⊥ PD (đpcm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107971
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68731
Đã trả lời bởi chuyên gia
68731 -
 Đã trả lời bởi chuyên gia
53018
Đã trả lời bởi chuyên gia
53018 -
 Đã trả lời bởi chuyên gia
47519
Đã trả lời bởi chuyên gia
47519 -
 Đã trả lời bởi chuyên gia
45631
Đã trả lời bởi chuyên gia
45631 -
 Đã trả lời bởi chuyên gia
45278
Đã trả lời bởi chuyên gia
45278 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38679
Đã trả lời bởi chuyên gia
38679 -
 Đã trả lời bởi chuyên gia
38337
Đã trả lời bởi chuyên gia
38337


