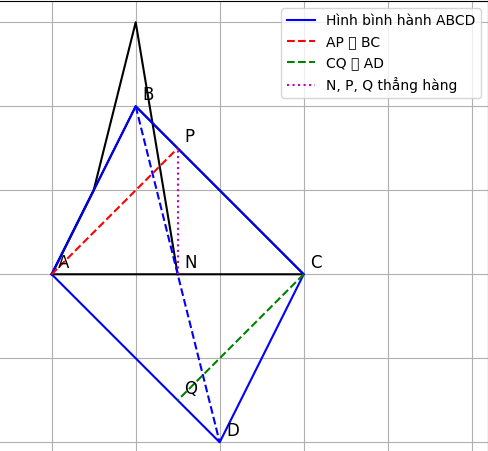
a) Chứng minh tứ giác ABCD là hình bình hành
Vì N là trung điểm của AC, nên: AN = NC
Lại có D thuộc tia BN sao cho DN = BN, suy ra:
N là trung điểm của BD.
⇒ N là trung điểm chung của hai đoạn AC và BD.
→ Trong tứ giác ABCD, nếu hai đường chéo cắt nhau tại trung điểm của mỗi đường, thì tứ giác đó là hình bình hành.
=> ABCD là hình bình hành.
b) Chứng minh ba điểm N, P, Q thẳng hàng
Ta có:
AP ⊥ BC
CQ ⊥ AD
Vì ABCD là hình bình hành nên: AD // BC
⇒ Hai đường vuông góc với AD và BC sẽ song song với nhau.
→ Suy ra: AP // CQ
Trong hình bình hành, các đường cao tương ứng song song, và trung điểm N của cạnh bên AC nằm giữa hai đường song song ấy.
=> Do đó, đường thẳng qua N song song với AP và CQ sẽ đi qua hai chân vuông góc P và Q.
=> N, P, Q thẳng hàng.
c) Điều kiện để ABCD là hình vuông
Vì ABCD là hình bình hành, để nó là hình vuông cần thêm:
Góc tại A bằng 90°, để nó trở thành hình chữ nhật.
Và thêm điều kiện AB = AD, để các cạnh bằng nhau.
→ Khi đó ABCD là hình vuông.
=> Tam giác ABC phải là tam giác vuông cân tại A và AB = AC.

Đề bài tóm tắt
Cho tam giác ABCABCABC nhọn có AB<ACAB < ACAB<AC.
Gọi NNN là trung điểm của ACACAC.
Lấy điểm DDD trên tia BNBNBN sao cho DN=BNDN = BNDN=BN.

Yêu cầu:
a) Chứng minh ABCDABCDABCD là hình bình hành.
b) Kẻ AP⊥BCAP \perp BCAP⊥BC tại PPP, CQ⊥ADCQ \perp ADCQ⊥AD tại QQQ. Chứng minh ba điểm N,P,QN, P, QN,P,Q thẳng hàng.
c) Tìm điều kiện để ABCDABCDABCD là hình vuông.

Câu a) Chứng minh tứ giác ABCD là hình bình hành
Phân tích:
Ta có NNN là trung điểm của ACACAC.
DDD nằm trên tia BNBNBN sao cho DN=BNDN = BNDN=BN → NNN cũng là trung điểm của BDBDBD.
Suy ra:
NNN là trung điểm của AC và BD.
⇒ Hai đường chéo ACACAC và BDBDBD cắt nhau tại trung điểm của mỗi đường.
→ Tứ giác ABCDABCDABCD là hình bình hành.

✅ Kết luận: ABCDABCDABCD là hình bình hành vì hai đường chéo cắt nhau tại trung điểm.

Câu b) Chứng minh N, P, Q thẳng hàng
Cho biết:
AP⊥BCAP \perp BCAP⊥BC tại PPP.
CQ⊥ADCQ \perp ADCQ⊥AD tại QQQ.
ABCDABCDABCD là hình bình hành → AD∥BCAD ∥ BCAD∥BC, AB∥CDAB ∥ CDAB∥CD.
Nhận xét:
Trong hình bình hành, các cạnh đối song song:

AD∥BCAD ∥ BCAD∥BC.
Do đó, AP⊥BC⇒AP⊥ADAP \perp BC \Rightarrow AP \perp ADAP⊥BC⇒AP⊥AD.
→ APAPAP vuông góc với cả ADADAD và BCBCBC.
Tương tự, CQ⊥AD⇒CQ⊥BCCQ \perp AD \Rightarrow CQ \perp BCCQ⊥AD⇒CQ⊥BC.

=> Hai đường cao từ AAA và CCC trong tam giác ABCABCABC và ADCADCADC cùng vuông góc với cạnh chung (ở đây là AD,BCAD, BCAD,BC), nên chúng nằm trong cùng một mặt phẳng và có cùng hướng vuông góc với đáy của hình bình hành.

Dễ thấy:
Trong hình bình hành, đường trung bình nối trung điểm của hai cạnh bên luôn song song với hai cạnh đáy.

Ở đây NNN là trung điểm của ACACAC.
Đường thẳng đi qua NNN song song với ADADAD cũng song song với BCBCBC.
Các điểm PPP và QQQ đều nằm trên đường vuông góc với AD,BCAD, BCAD,BC nên chúng nằm trên đường qua NNN song song với ADADAD.

✅ Kết luận: Ba điểm N,P,QN, P, QN,P,Q thẳng hàng.

Câu c) Điều kiện để tứ giác ABCD là hình vuông
Ta đã biết ABCDABCDABCD là hình bình hành.
Muốn nó là hình vuông, cần:

Các cạnh bằng nhau.
Có một góc vuông.
Trong hình bình hành, chỉ cần một góc vuông → là hình chữ nhật.
Nếu thêm hai cạnh kề bằng nhau, nó sẽ là hình vuông.

→ Ở đây, điều kiện cần là:

△ABC\triangle ABC△ABC phải cân tại A, tức là AB=ACAB = ACAB=AC.
Kiểm tra hợp lý:
Nếu AB=ACAB = ACAB=AC thì tam giác ABCABCABC cân tại AAA.
⇒ NNN là trung điểm của ACACAC, đối xứng qua đường trung trực của ACACAC.
⇒ Dễ thấy ABCDABCDABCD vừa có các cạnh bằng nhau, vừa có góc vuông (do tính chất đối xứng),
nên ABCDABCDABCD là hình vuông.

✅ Kết luận cuối cùng:

Để tứ giác ABCDABCDABCD là hình vuông, tam giác ABCABCABC phải cân tại A, tức là AB=ACAB = ACAB=AC.

✨ Tóm tắt đáp án:
Câu
Kết quả chính
Lý do
a)
ABCDABCDABCD là hình bình hành
Vì hai đường chéo cắt nhau tại trung điểm
b)
N,P,QN, P, QN,P,Q thẳng hàng
Vì APAPAP và CQCQCQ đều vuông góc với hai cạnh song song AD,BCAD, BCAD,BC
c)
Tam giác ABCABCABC cân tại A
Khi đó ABCDABCDABCD là hình vuông