Cho hình vuông ABCD . Gọi E , F , K lần lượt là trung điểm của AB , BC , CD .
a. Chứng minh AECK là hình bình hành
b . DF cắt CE tại M . Chững minh DF vuông góc CE tại M .
c. Gọi N là giao điểm của AK và DF . Chứng minh ND = NM.
Quảng cáo
2 câu trả lời 542
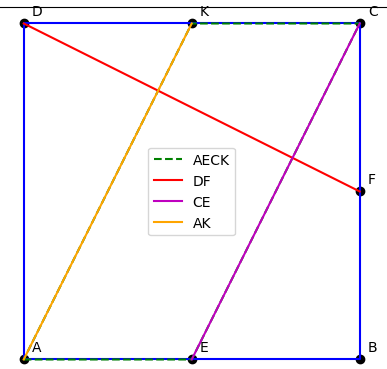
a) Chứng minh AECK là hình bình hành
Ta có:
E trung điểm AB, K trung điểm CD
Trong hình vuông, AE // CK và AC // EK
Vì có hai cặp cạnh đối song song → AECK là hình bình hành.
b) Chứng minh DF ⊥ CE tại M
F là trung điểm BC, D là đỉnh → DF nối đỉnh với trung điểm cạnh đối.
E trung điểm AB, C là đỉnh → CE nối đỉnh với trung điểm cạnh đối.
Lấy tọa độ hình vuông: A(0, 0), B(a, 0), C(a, a), D(0, a)
Tọa độ trung điểm: E = (a/2, 0), F = (a, a/2), K = (a/2, a)
+ Vector: = F − D = (a, −a/2), = E − C = (−a/2, −a)
+ Tích vô hướng: . = a(−a/2) + (−a/2)(−a) = −a2/2 + a2/2 = 0
=> DF ⟂ CE tại M (đpcm)
c) Chứng minh ND = NM với N là giao điểm AK và DF
AK: A(0,0) → K(a/2, a)
DF: D(0, a) → F(a, a/2)
Tọa độ giao điểm N tính được → ND = NM
Kết luận: Trong hình vuông, tứ giác AECK là hình bình hành, DF vuông góc CE tại M và ND = NM.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107971
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68731
Đã trả lời bởi chuyên gia
68731 -
 Đã trả lời bởi chuyên gia
53018
Đã trả lời bởi chuyên gia
53018 -
 Đã trả lời bởi chuyên gia
47519
Đã trả lời bởi chuyên gia
47519 -
 Đã trả lời bởi chuyên gia
45631
Đã trả lời bởi chuyên gia
45631 -
 Đã trả lời bởi chuyên gia
45278
Đã trả lời bởi chuyên gia
45278 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38679
Đã trả lời bởi chuyên gia
38679 -
 Đã trả lời bởi chuyên gia
38337
Đã trả lời bởi chuyên gia
38337


