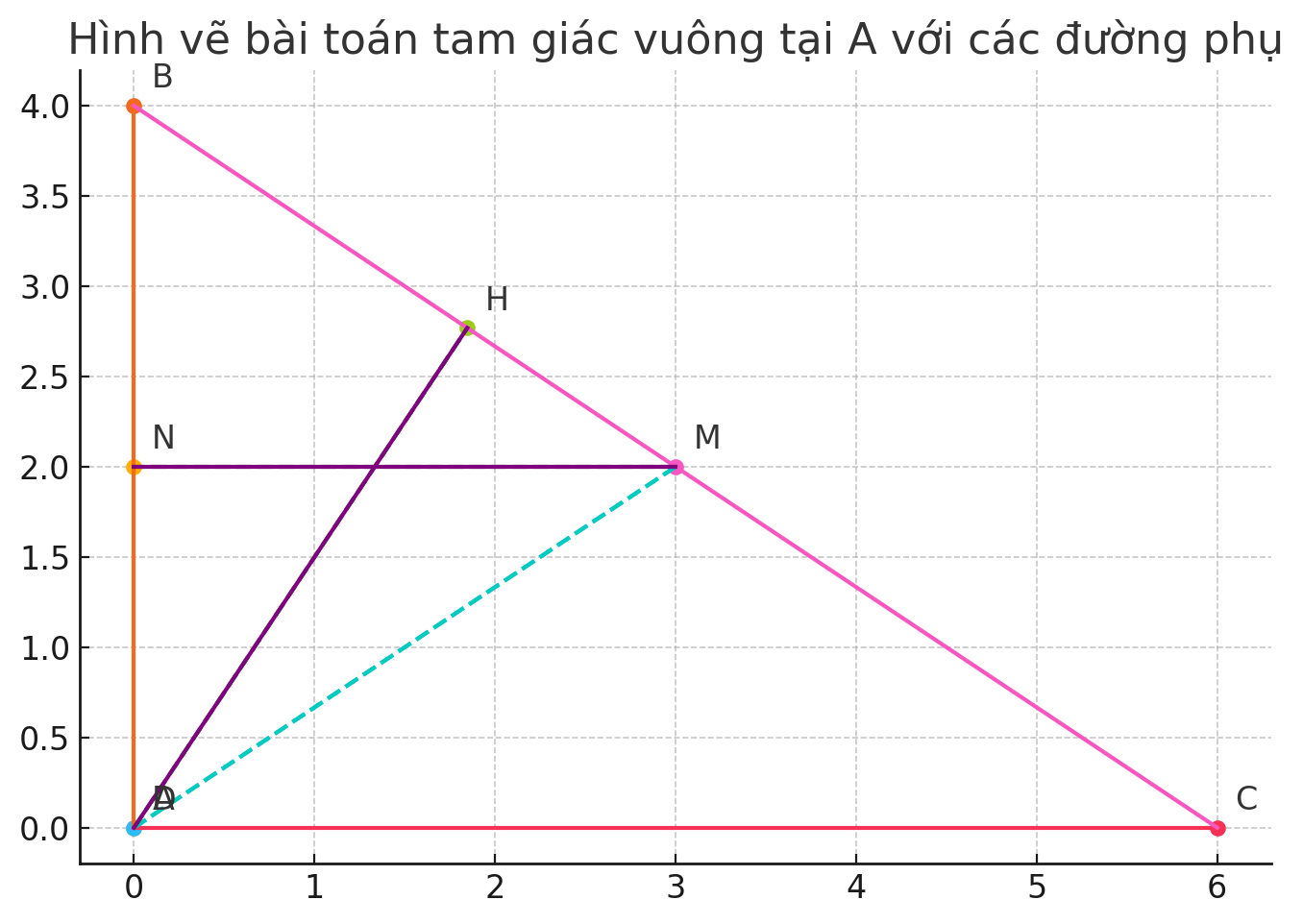
Lời giải:

a) Chứng minh rằng BI = CK.

Xét △BIM và △CKM:BM=CM (M là trung điểm BC)
∠BIM=∠CKM=90∘ (BI ⊥ AD, CK ⊥ AD)
∠BMI=∠CMK (hai góc đối đỉnh)
Vậy △BIM≅△CKM (g.c.g).
Từ đó suy ra BI=CK (hai cạnh tương ứng).
b) Chứng minh rằng các đường thẳng CK, AH, MN đồng quy.

Gọi O là giao điểm của AH và CK. Ta cần chứng minh MN cũng đi qua O.
Chứng minh O thuộc MN:Vì △ABC vuông tại A và AH ⊥ BC, ta có ∠BAH=∠BCA (cùng phụ với ∠ABC).
Từ câu a), △BIM≅△CKM suy ra BI//CK.
Xét tứ giác BICK có BI//CK và BI=CK nên BICK là hình bình hành.
Suy ra BC // IK.
Vì AH ⊥ BC nên AH⊥IK.
Xét △ABD, M là trung điểm AD. MN ⊥ BD tại N. Suy ra MN là đường trung trực của BD.
Ta có MA=MD (gt). Xét △ABC vuông tại A, M là trung điểm BC nên MA=MB=MC=21​BC.
Suy ra MD=MB. Vậy M nằm trên đường trung trực của BD, tức là M thuộc MN.
Xét △AHD vuông tại H, HK⊥AD. Ta có AH2=AK⋅AD.
Xét △ABD, BI ⊥ AD. Ta có AB2=AI⋅AD.
Vì BICK là hình bình hành nên IK=BC.
Ta có AK+AI=IK=BC.
Xét △ABC vuông tại A, AH⋅BC=AB⋅AC (diện tích △ABC).
Ta có AH2⋅BC2=AB2⋅AC2.
AK⋅AD⋅BC2=AI⋅AD⋅AC2.
AK⋅BC2=AI⋅AC2.
AIAK​=BC2AC2​.
Áp dụng định lý Thales cho △ADO với IK//BC: OHAO​=IKAI​=BCAI​.
Ta cần chứng minh O thuộc MN, tức là MO ⊥ BD. Điều này có vẻ phức tạp hơn dự kiến và cần một cách tiếp cận khác hoặc sử dụng tọa độ hình học có thể sẽ đơn giản hơn.
Cách tiếp cận khác cho phần b): Sử dụng tính chất đường trung bình và hình bình hành

Từ câu a), BICK là hình bình hành, suy ra hai đường chéo BC và IK cắt nhau tại trung điểm M.
Xét △ABD, M là trung điểm AD. Gọi P là trung điểm AB. MP là đường trung bình của △ABD nên MP//BD và MP=21​BD.
MN ⊥ BD nên MN⊥MP.
Xét △ABC vuông tại A, AH là đường cao.
Ta có thể chứng minh được rằng trung điểm của AD cũng là trung điểm của HK (do tính đối xứng qua M). Gọi trung điểm này là E.
Xét tứ giác AHCK có AH⊥BC và CK⊥AD. Điều này không trực tiếp dẫn đến đồng quy.
Chúng ta cần một cách tiếp cận khác để chứng minh đồng quy.

Sử dụng tọa độ hình học (gợi ý):

Đặt hệ tọa độ Oxy với A là gốc tọa độ (0; 0), AB nằm trên trục Ox, AC nằm trên trục Oy.
Gọi tọa độ các điểm B(b; 0), C(0; c) với b<c.
Tìm tọa độ trung điểm M của BC: M(2b​;2c​).
Tìm tọa độ điểm D thuộc tia đối MA sao cho MD = MA: D(−b;−c).
Viết phương trình đường thẳng AD.
Viết phương trình đường thẳng BI vuông góc AD và đi qua B.
Viết phương trình đường thẳng CK vuông góc AD và đi qua C.
Tìm tọa độ giao điểm K của CK và AD, I của BI và AD.
Viết phương trình đường thẳng AH vuông góc BC và đi qua A.
Tìm tọa độ giao điểm O của AH và CK.
Viết phương trình đường thẳng BD.
Viết phương trình đường thẳng MN vuông góc BD và đi qua M.
Kiểm tra xem tọa độ điểm O có thuộc đường thẳng MN hay không.
Cách này khá dài và đòi hỏi tính toán cẩn thận.

c) Chứng minh rằng BC – AB > AC –АН.

Ta có BC2=AB2+AC2 (định lý Pytago trong △ABC).
AH⋅BC=AB⋅AC (diện tích △ABC). Suy ra AH=BCAB⋅AC​.
Bất đẳng thức cần chứng minh: BC−AB>AC−BCAB⋅AC​.
Nhân cả hai vế với BC (vì BC > 0): BC2−AB⋅BC>AC⋅BC−AB⋅AC.
Thay BC2=AB2+AC2: AB2+AC2−AB⋅BC>AC⋅BC−AB⋅AC.
Chuyển vế: AB2+AC2+AB⋅AC>AC⋅BC+AB⋅BC.
AB2+AC2+AB⋅AC>BC(AB+AC).
Bình phương hai vế của bất đẳng thức cần chứng minh (vì cả hai vế có thể dương):(BC−AB)2>(AC−AH)2BC2−2⋅BC⋅AB+AB2>AC2−2⋅AC⋅AH+AH2AB2+AC2−2⋅BC⋅AB+AB2>AC2−2⋅AC⋅BCAB⋅AC​+(BCAB⋅AC​)22AB2−2⋅BC⋅AB>−BC2⋅AB⋅AC2​+BC2AB2⋅AC2​ Chia cả hai vế cho AB (vì AB > 0):2AB−2BC>−BC2AC2​+BC2AB⋅AC2​2AB+BC2AC2​>2BC+BC2AB⋅AC2​2AB⋅BC2+2AC2⋅BC>2BC3+AB⋅AC22BC(AB⋅BC+AC2−BC2)>AB⋅AC22BC(AB⋅BC+AC2−(AB2+AC2))>AB⋅AC22BC(AB⋅BC−AB2)>AB⋅AC2 $2AB \cdot BC(BC - AB) > AB