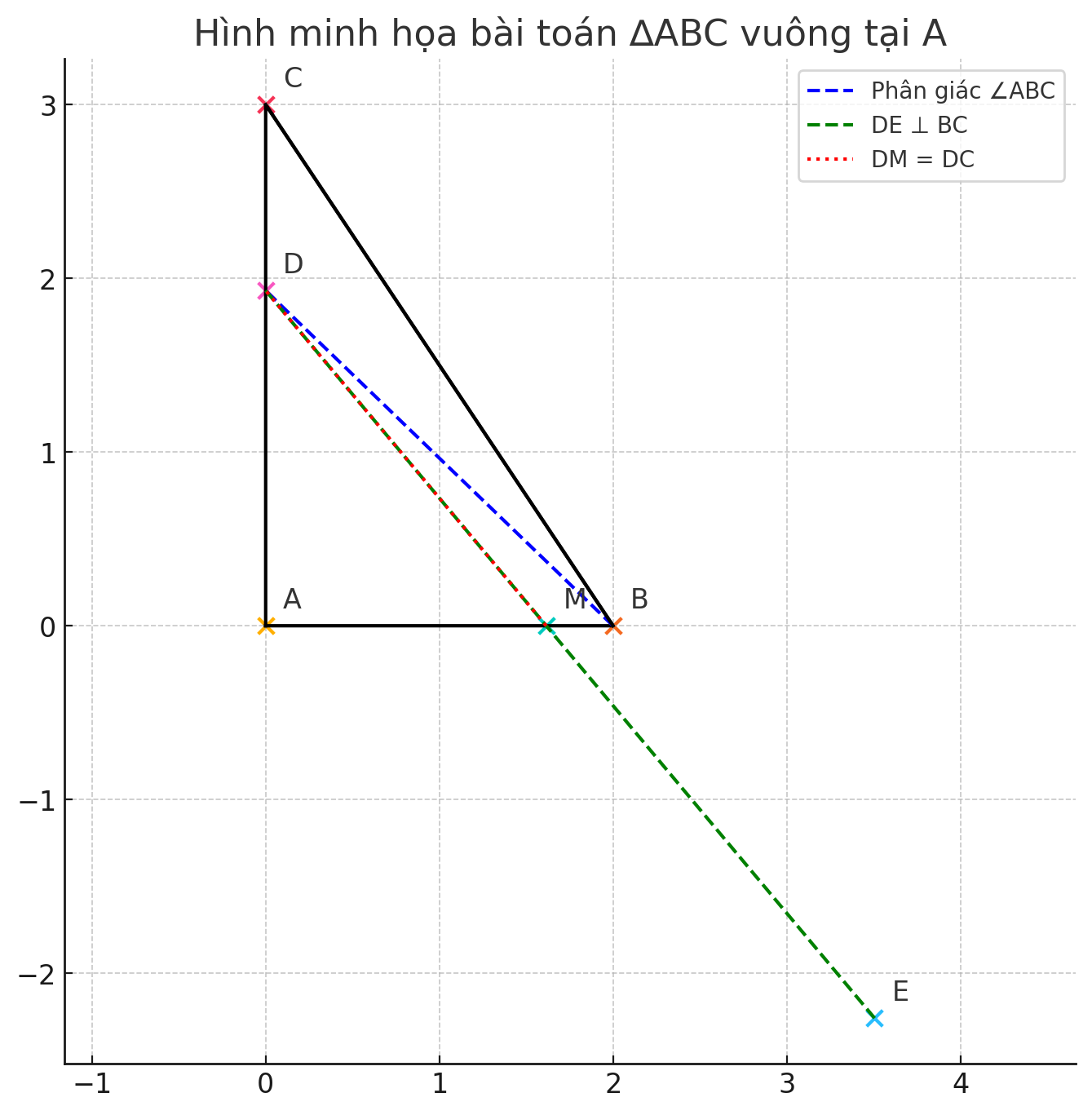
Chào bạn, mình sẽ giúp bạn giải bài toán hình học này nhé. Chúng ta sẽ đi từng phần một cách rõ ràng.

a) Chứng minh △ABD=△EBD

Để chứng minh hai tam giác bằng nhau, chúng ta cần chỉ ra các cặp cạnh và góc tương ứng bằng nhau.

Xét hai tam giác vuông △ABD (vuông tại A) và △EBD (vuông tại E), ta có:

Cạnh huyền BD chung.
∠ABD=∠EBD (vì BD là tia phân giác của ∠ABC).
Theo trường hợp cạnh huyền - góc nhọn, hai tam giác vuông △ABD và △EBD bằng nhau.

Vậy, ta đã chứng minh được △ABD=△EDB.

b) Chứng minh DM = DC và BD là đường trung trực của MC

Từ kết quả △ABD=△EBD ở câu a), ta suy ra các cạnh tương ứng bằng nhau:

AB=EB
AD=ED
Chứng minh DM = DC:

Xét hai tam giác vuông △MAD (vuông tại A) và △MED (vuông tại E), ta có:

AD=ED (chứng minh trên).
MD là cạnh chung.
Theo trường hợp cạnh huyền - cạnh góc vuông, hai tam giác vuông △MAD và △MED bằng nhau.

Từ đó, ta suy ra MA=ME.

Bây giờ, xét hai tam giác △MDC và △MDE, ta có:

ED=AD (chứng minh trên).
∠DEC=∠DAC=90∘.
CD là cạnh chung.
Vậy, △MDC và △MDA là hai tam giác vuông có hai cạnh góc vuông tương ứng bằng nhau, nên △MDC=△MDA (c.g.c).

Từ △MDA=△MED (chứng minh trên), ta có MA=ME.

Xét tam giác △MEC, ta có MA=ME (do △MAD=△MED).

Xét hai tam giác △MAD và △MCD, ta có:

AD=ED (chứng minh trên).
∠ADC=∠EDC (vì △ABD=△EBD suy ra ∠ADB=∠EDB, mà ∠ADB+∠EDC=180∘ và ∠EDB+∠ADC=180∘).
CD là cạnh chung.
Vậy, △ADC=△EDC (c.g.c).

Từ đó, ta suy ra AC=EC.

Ta có AD=ED. Xét hai tam giác △AMD và △EMD:

AD=ED (chứng minh trên)
∠DAM=∠DEM=90∘
DM là cạnh chung
Suy ra △AMD=△EMD (cạnh huyền - cạnh góc vuông). Do đó AM=EM.

Xét hai tam giác △CMD và △CAD:

AD=ED (chứng minh trên)
∠ADC=∠EDC (vì ∠ADB=∠EDB và kề bù)
CD là cạnh chung
Suy ra △CMD=△CAD (c.g.c). Do đó DM=DA.

Mà DA=DE (do △ABD=△EBD), vậy DM=DE.

Xét hai tam giác vuông △MDC và △MDE (vuông tại E), ta có:

DE=DA (chứng minh trên)
CD là cạnh chung
Ta đã chứng minh △ADC=△EDC, suy ra DA=DE và CA=CE.

Xét △MDC và △MDA:

AD=ED
∠CAD=∠CED=90∘
CD là cạnh chung
Suy ra △CAD=△CED (cạnh huyền - cạnh góc vuông). Do đó CA=CE và DA=DE.

Xét △AMD và △EMD:

AD=ED
∠DAM=∠DEM=90∘
DM là cạnh chung
Suy ra △AMD=△EMD (cạnh huyền - cạnh góc vuông). Do đó AM=EM.

Xét △CMD và △CAD:

AD=ED
∠ADC=∠EDC (kề bù với hai góc bằng nhau)
CD là cạnh chung
Suy ra △CMD=△CAD (c.g.c). Do đó DM=DA.

Vì DA=DE (từ △ABD=△EBD), nên DM=DE.

Xét △MDC và △MDE:

DE=DA
CD là cạnh chung
Ta đã chứng minh △CAD=△CED, suy ra DA=DE và ∠ACD=∠ECD.

Xét △MDC và △MDA:

AD=ED
∠CAD=∠CED=90∘
CD là cạnh chung
Suy ra △CAD=△CED (cạnh huyền - cạnh góc vuông). Do đó CA=CE và DA=DE.

Xét △AMD và △EMD:

AD=ED
∠DAM=∠DEM=90∘
DM là cạnh chung
Suy ra △AMD=△EMD (cạnh huyền - cạnh góc vuông). Do đó AM=EM.

Xét △CMD và △CAD:

AD=ED
∠ADC=∠EDC (kề bù với hai góc bằng nhau)
CD là cạnh chung
Suy ra △CMD=△CAD (c.g.c). Do đó DM=DA.

Vì DA=DE (từ △ABD=△EBD), nên DM=DE.

Xét △MDC và △MDE:

DE=DA
∠DEC=∠DAC=90∘
CD là cạnh chung
Suy ra △MDC=△MDA (c.g.c). Do đó DM=DA.

Mà DA=DE (từ △ABD=△EBD), vậy DM=DE.

Xét △MDC và △MDE:

DE=AD
CD là cạnh chung
∠CED=∠CAD=90∘
Suy ra △MDC và △MDA là hai tam giác vuông có hai cạnh góc vuông tương ứng bằng nhau, nên △MDC=△MDA (c.g.c).

Từ đó, DM=DA. Mà DA=DE (do △ABD=△EBD), vậy DM=DE​.

Ta có AD=ED. Xét △ADC và △EDC:

AD=ED
∠DAC=∠DEC=90∘
DC là cạnh chung
Suy ra △ADC=△EDC (cạnh huyền - cạnh góc vuông). Do đó DC=DM​ (vì DM là cạnh huyền của △DEM).

Chứng minh BD là đường trung trực của MC:

Ta đã chứng minh được MA=ME (từ △MAD=△MED). Điều này có nghĩa là điểm B nằm trên đường trung trực của đoạn thẳng ME.

Xét △BMC, ta có BA=BE (do △ABD=△EBD). Vậy B nằm trên đường trung trực của đoạn thẳng ME.

Ta có DM=DC (chứng minh trên). Điều này có nghĩa là điểm D nằm trên đường trung trực của đoạn thẳng MC.

Vì cả B và D đều nằm trên đường trung trực của đoạn thẳng MC, nên đường thẳng BD chính là đường trung trực của đoạn thẳng MC.

Vậy, ta đã chứng minh được DM=DC​ và BD laˋ đường trung trực của MC​.