Quảng cáo
2 câu trả lời 2279
Đặt hệ trục tọa độ
Cho mặt đáy ABCD là hình vuông cạnh \( a = 2 \) (để dễ tính), tọa độ các điểm như sau:
- \( A(0, 0, 0), B(2, 0, 0), C(2, 2, 0), D(0, 2, 0) \)
- ⇒ \( O = (1,1,0) \) – giao điểm 2 đường chéo
- \( S = (1,1,h) \) – vì thẳng đứng trên O
- Trung điểm \( M \) của AB ⇒ \( M = (1, 0, 0) \)
Xét góc giữa 2 vectơ \( \vec{OM} \) và \( \vec{OD} \)
- \( \vec{OM} = (1,0,0) - (1,1,0) = (0, -1, 0) \)
- \( \vec{OD} = (0,2,0) - (1,1,0) = (-1,1,0) \)
Góc giữa 2 vectơ này chính là góc nhị diện giữa mặt (MSO) và (DSO) tại cạnh chung \( SO \)
Tính góc giữa hai vectơ
Sử dụng công thức:
\[
\cos \theta = \frac{\vec{OM} \cdot \vec{OD}}{|\vec{OM}| \cdot |\vec{OD}|}
\]
- Tích vô hướng:
\[
\vec{OM} \cdot \vec{OD} = (0)(-1) + (-1)(1) + (0)(0) = -1
\]
- Độ dài:
\[
|\vec{OM}| = \sqrt{0^2 + (-1)^2 + 0^2} = 1
|\vec{OD}| = \sqrt{(-1)^2 + 1^2 + 0^2} = \sqrt{2}
\]
\[
\Rightarrow \cos \theta = \frac{-1}{1 \cdot \sqrt{2}} = -\frac{1}{\sqrt{2}}
\Rightarrow \theta = \arccos \left( -\frac{1}{\sqrt{2}} \right) = 135^\circ
\]
Đáp án cuối cùng:
Số đo góc nhị diện [M,SO,D] là \( \boxed{135^\circ} \)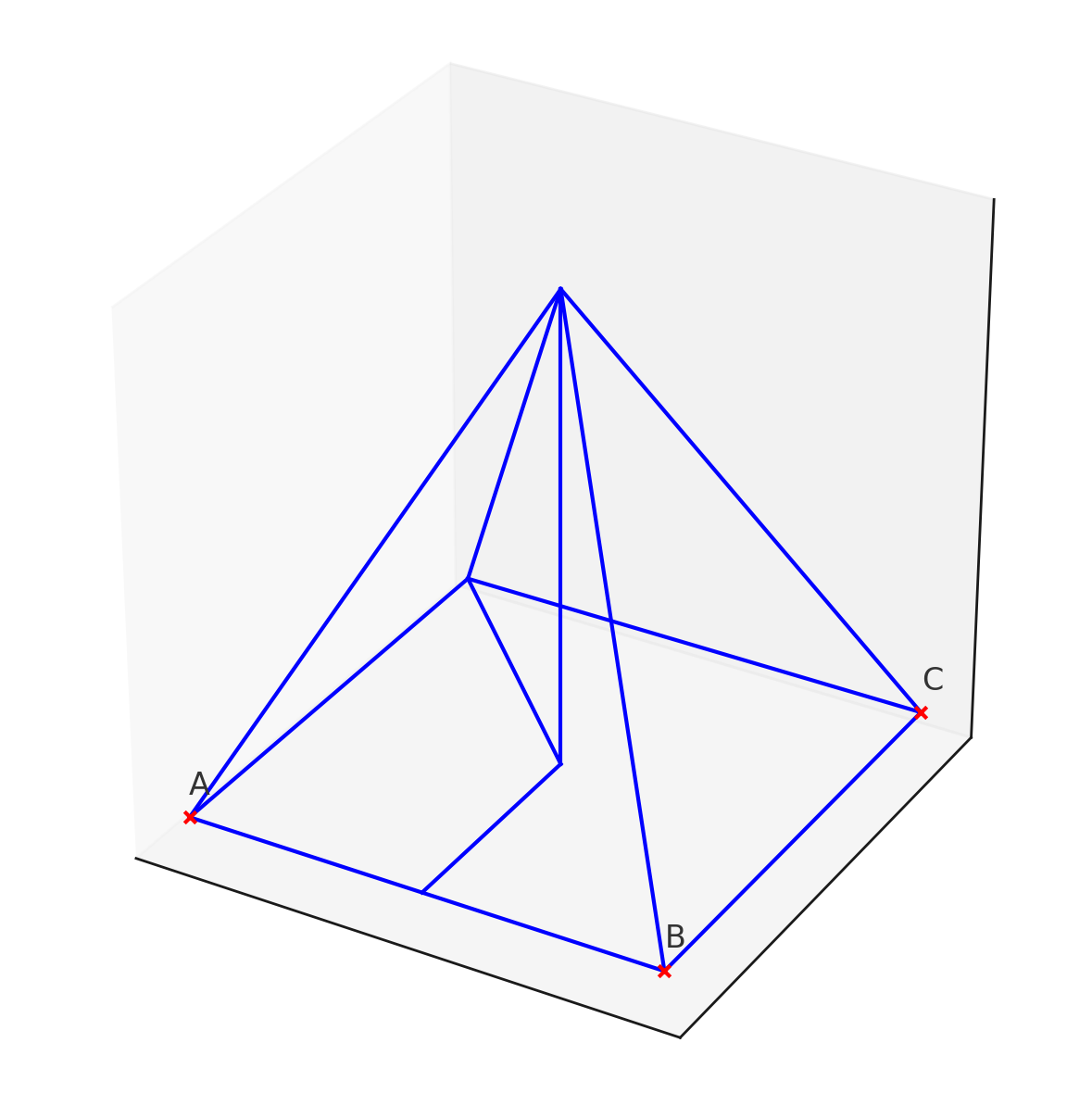
Hình chóp tứ giác đều SABCD có đáy là hình vuông và SO vuông góc với đáy.
Góc giữa (MSO) và (DSO) chính là góc giữa MO và DO trong mặt phẳng chứa hai đường thẳng này.
Xét mặt phẳng (ABCD), ta có:
O là tâm hình vuông ABCD.
M là trung điểm AB.
Góc MOD = 45° vì OM là phân giác góc AOB và AOB = 90° (đường chéo hình vuông).
Vậy góc nhị diện [M, SO, D] = 45°.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134901
Đã trả lời bởi chuyên gia
134901 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
76057
Đã trả lời bởi chuyên gia
76057 -
 Đã trả lời bởi chuyên gia
71711
Đã trả lời bởi chuyên gia
71711 -
 Đã trả lời bởi chuyên gia
47598
Đã trả lời bởi chuyên gia
47598


