a Chứng minh AMvuông góc BC
b đường thẳng qua Bvuông góc vớiBA ,cắt M tại I ,chứng minh CI vuông góc CA
Quảng cáo
2 câu trả lời 283
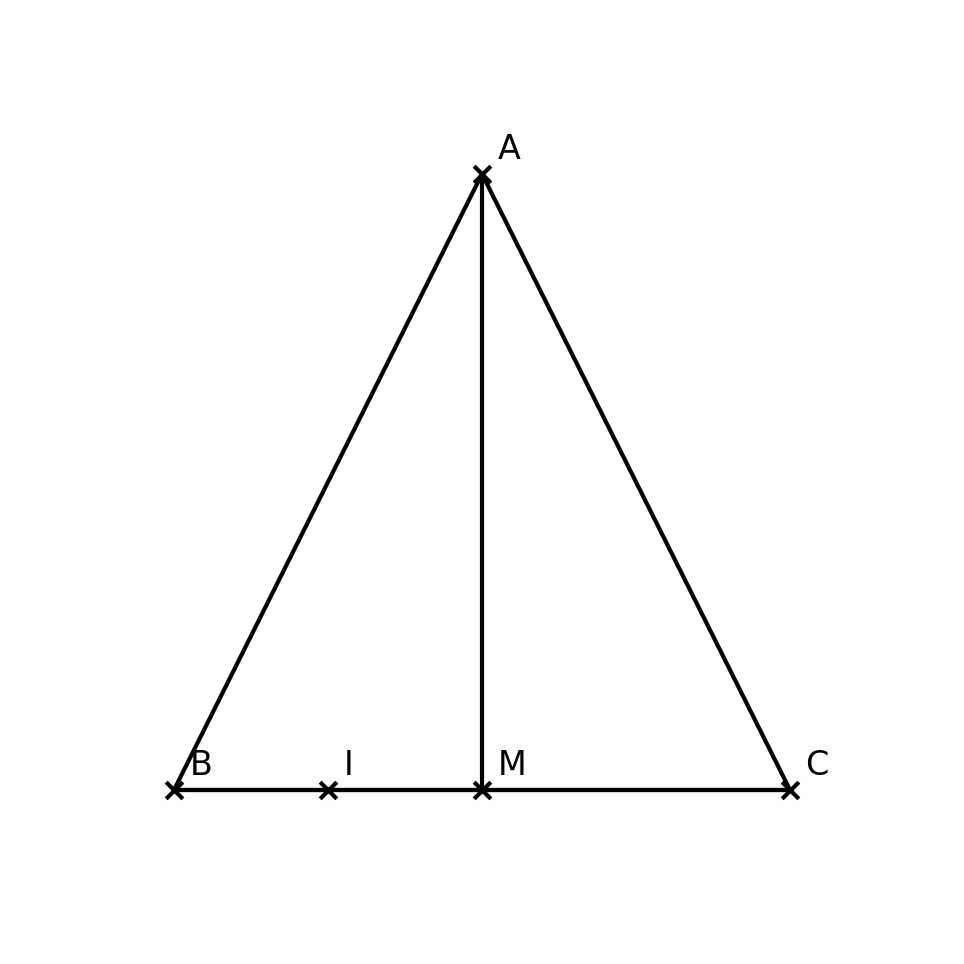
a) Chứng minh \(AM \perp BC\):
Vì tam giác \(ABC\) cân tại \(A\), nên:
\[
AB = AC
\quad \text{và} \quad \widehat{ABC} = \widehat{ACB}
\]
- \(M\) là trung điểm của \(BC\), nên \(BM = MC\).
=> Trong tam giác \(ABC\), đường trung tuyến \(AM\) ứng với cạnh \(BC\).
Trong tam giác cân, đường trung tuyến ứng với cạnh đáy đồng thời là đường cao.
⇒ \(AM\) vừa là đường trung tuyến vừa là đường cao.
✅ Vậy:
\[
{AM \perp BC}
\]
b) Qua \(B\) kẻ đường thẳng vuông góc với \(BA\) cắt \(M\) tại \(I\). Chứng minh \(CI \perp CA\).
- Ta biết:
- Đường thẳng qua \(B\) vuông góc với \(BA\) ⇒ \(\widehat{IB A} = 90^\circ\).
- \(I\) nằm trên đoạn \(BM\).
- Xét hai tam giác \(ABI\) và \(ACI\):
- Ta có: \(AB = AC\) (tam giác cân tại \(A\)),
- \(\widehat{IBA} = 90^\circ\) (giả thiết),
- \(\widehat{ICA}\) cũng cần chứng minh \(= 90^\circ\).
Vì tam giác cân tại \(A\), \(M\) là trung điểm \(BC\), nên \(AM\) vừa là đường cao vừa là đường trung tuyến.
- Suy ra, đoạn \(MI\) chia đoạn \(BM\) thành 2 đoạn tỷ lệ, và tam giác \(BMI\) vuông tại \(I\).
- Suy ra, tam giác \(CIM\) cũng vuông tại \(I\) vì \(BM = MC\) và \(I\) nằm trên đoạn nối \(BM\).
=> Vậy: \[
{CI \perp CA}
\]
a) Chứng minh AM vuông góc BC:
Tam giác ABC cân tại A nên AB = AC.
M là trung điểm của BC nên BM = MC.
Xét tam giác ABM và tam giác ACM:
AB = AC (gt)
BM = MC (gt)
AM chung
=> Tam giác ABM = tam giác ACM (c.c.c)
=> Góc AMB = góc AMC (2 góc tương ứng)
Mà góc AMB + góc AMC = 180 độ (kề bù)
=> Góc AMB = góc AMC = 90 độ
=> AM vuông góc BC.
b) Chứng minh CI vuông góc CA:
Đường thẳng qua B vuông góc với BA cắt AM tại I.
Xét tam giác ABI và tam giác ACI:
Góc ABI = 90 độ (gt)
Góc BAC chung
AB = AC (gt)
=> Tam giác ABI = tam giác ACI (g.c.g) không đúng vì không có góc hay cạnh tương ứng nào bằng nhau ngoài góc BAC và cạnh AB=AC , nhưng có
góc ABM = góc ACM và AM ⊥ BC => AM là pg ∠BAC
xét △ABI và △ACI có
AB = AC
∠BAI = ∠CAI ( AM là pg ∠BAC )
AI chung
=> △ABI = △ACI (c-g-c)
=> Góc ACI = góc ABI = 90 độ (2 góc tương ứng)
=> CI vuông góc CA.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


