a) Chứng minh: tam giác AHM đồng dạng với tam giác ABH và \( AH^2 = AM \times AB \)

Chứng minh đồng dạng \( \triangle AHM \sim \triangle ABH \):

- Xét hai tam giác \( AHM \) và \( ABH \):
- Có: \( \widehat{AHM} = \widehat{ABH} = 90^\circ \) (giả thiết kẻ đường vuông góc).
- \( \widehat{MAH} = \widehat{BAH} \) (chung góc \( A \)).

→ Theo trường hợp góc – góc (g.g), ta có:
\[
\triangle AHM \sim \triangle ABH
\]
(đồng dạng).

Chứng minh \( AH^2 = AM \times AB \):

Vì \( \triangle AHM \sim \triangle ABH \), nên tỉ số các cạnh tương ứng bằng nhau:
\[
\frac{AH}{AB} = \frac{AM}{AH}
\]

Nhân chéo:
\[
AH^2 = AM \times AB
\]
 Điều phải chứng minh.

b) Tính \( AM \) và \( MN \)

Tính AM

Từ công thức vừa chứng minh:

\[
AH^2 = AM \times AB
\]
Thay số vào:

\[
12^2 = AM \times 15
\]
\[
144 = 15 \times AM
\]
\[
AM = \frac{144}{15} = 9,6\ \text{cm}
\]

Tính MN

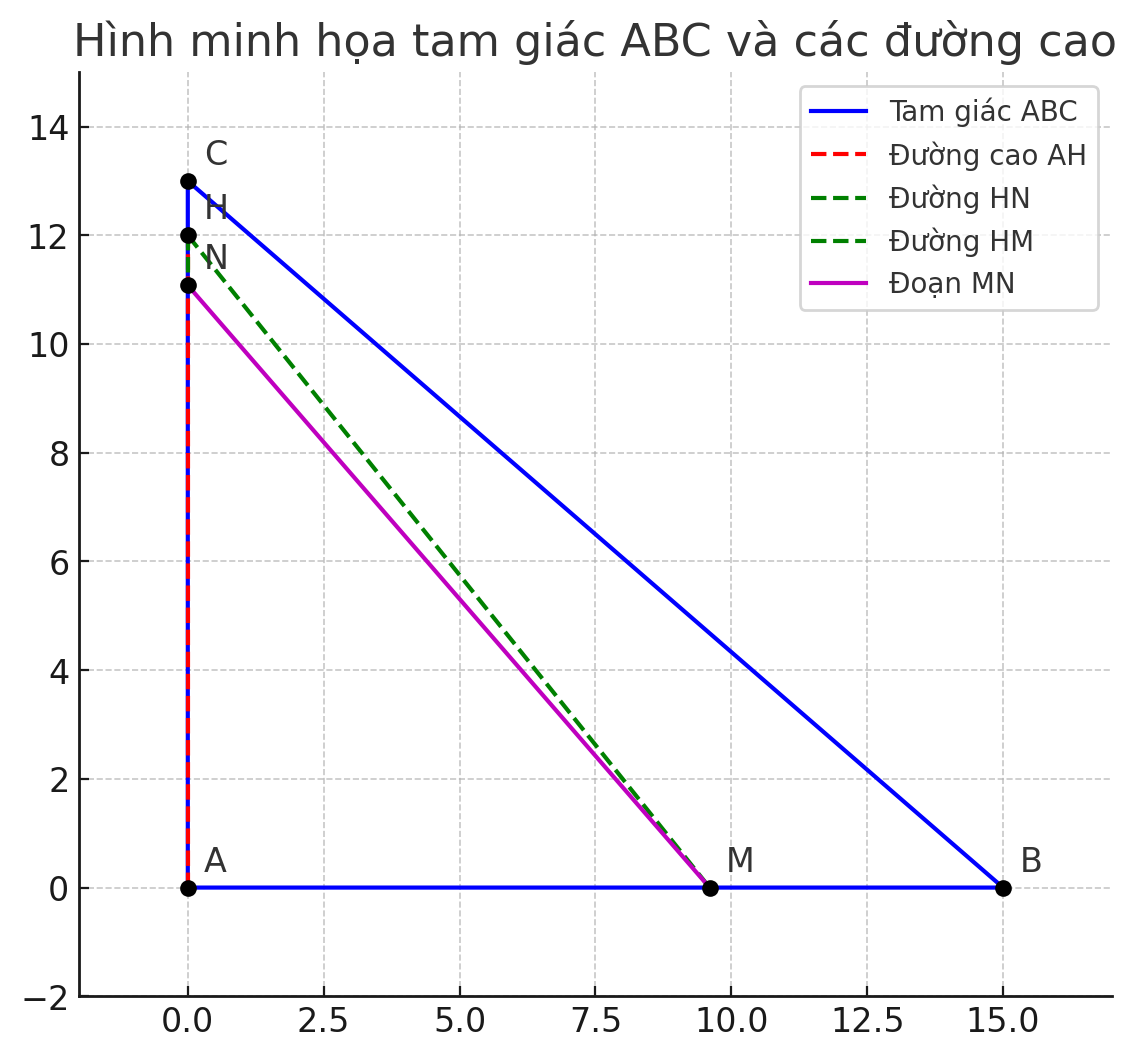
Chú ý rằng: \( MN \) là đoạn thẳng giữa hai chân đường vuông góc hạ từ \( H \) lên hai cạnh \( AB \) và \( AC \).

Mà trong tam giác vuông \( AHN \) và \( AHM \):
- \( MN = BM + CN \) (theo hình học bổ sung).

Tính BM và CN bằng công thức đường cao trong tam giác vuông:

Trong tam giác \( ABH \) vuông tại \( H \):
\[
AM \times AB = AH^2
\]
(đã dùng trên).

Tương tự trong tam giác \( ACH \):
\[
AN \times AC = AH^2
\]
(cách chứng minh giống hệt phần a)).

Vậy ta có:

\[
AN \times AC = 144
\]

Thay \( AC = 13\ \text{cm} \), tính \( AN \):

\[
AN = \frac{144}{13} \approx 11,08\ \text{cm}
\]

Bây giờ:

- Trên \( AB \): từ A đến M là \( AM = 9,6\ \text{cm} \), nên BM = AB – AM:
\[
BM = 15 - 9,6 = 5,4\ \text{cm}
\]

- Trên \( AC \): từ A đến N là \( AN = 11,08\ \text{cm} \), nên NC = AC – AN:
\[
NC = 13 - 11,08 = 1,92\ \text{cm}
\]

Vậy:
\[
MN = BM + NC = 5,4 + 1,92 = 7,32\ \text{cm}
\]

| Ý hỏi | Đáp án |
|:--|:--|
| a | \( \triangle AHM \sim \triangle ABH \), và \( AH^2 = AM \times AB \) |
| b | \( AM = 9,6\ \text{cm} \), \( MN = 7,32\ \text{cm} \) |