Quảng cáo
1 câu trả lời 165
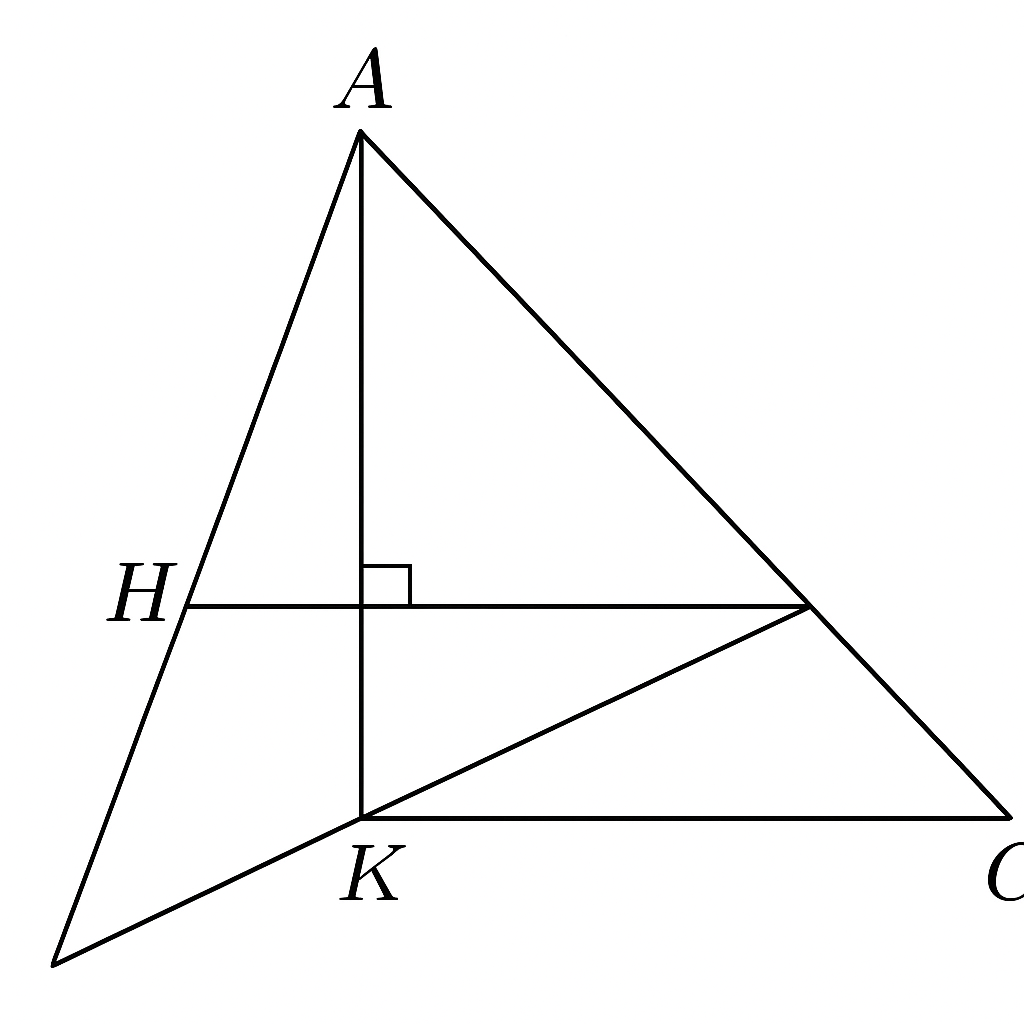
Chứng minh: Tam giác AHK có diện tích bằng diện tích tam giác ABC
Cách 1: So sánh diện tích
- Diện tích tam giác \( ABC \):
\[
S_{ABC} = \frac{1}{2} \cdot AB \cdot CK = \frac{1}{2} \cdot AC \cdot BH
\]
- Diện tích tam giác \( AHK \):
\[
S_{AHK} = \frac{1}{2} \cdot AH \cdot AK \cdot \sin(\angle HAK)
\]
Cách 2: Chứng minh AHK và ABC đồng dạng và có tỉ lệ bằng 1 ⇒ bằng nhau
Xét tam giác ABC và tam giác AHK
- \( \angle HAK = \angle BAC \) (góc chung)
- \( \angle AHK = 90^\circ - \angle C \), \( \angle ABC = 90^\circ - \angle C \)
- Tương tự, \( \angle AKH = 90^\circ - \angle B \), \( \angle ACB = 90^\circ - \angle B \)
⇒ Ba góc tương ứng bằng nhau
\[
\triangle AHK \sim \triangle ABC
\]
Nếu chứng minh thêm tỉ số đồng dạng = 1, thì:
\[
\triangle AHK \cong \triangle ABC
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


