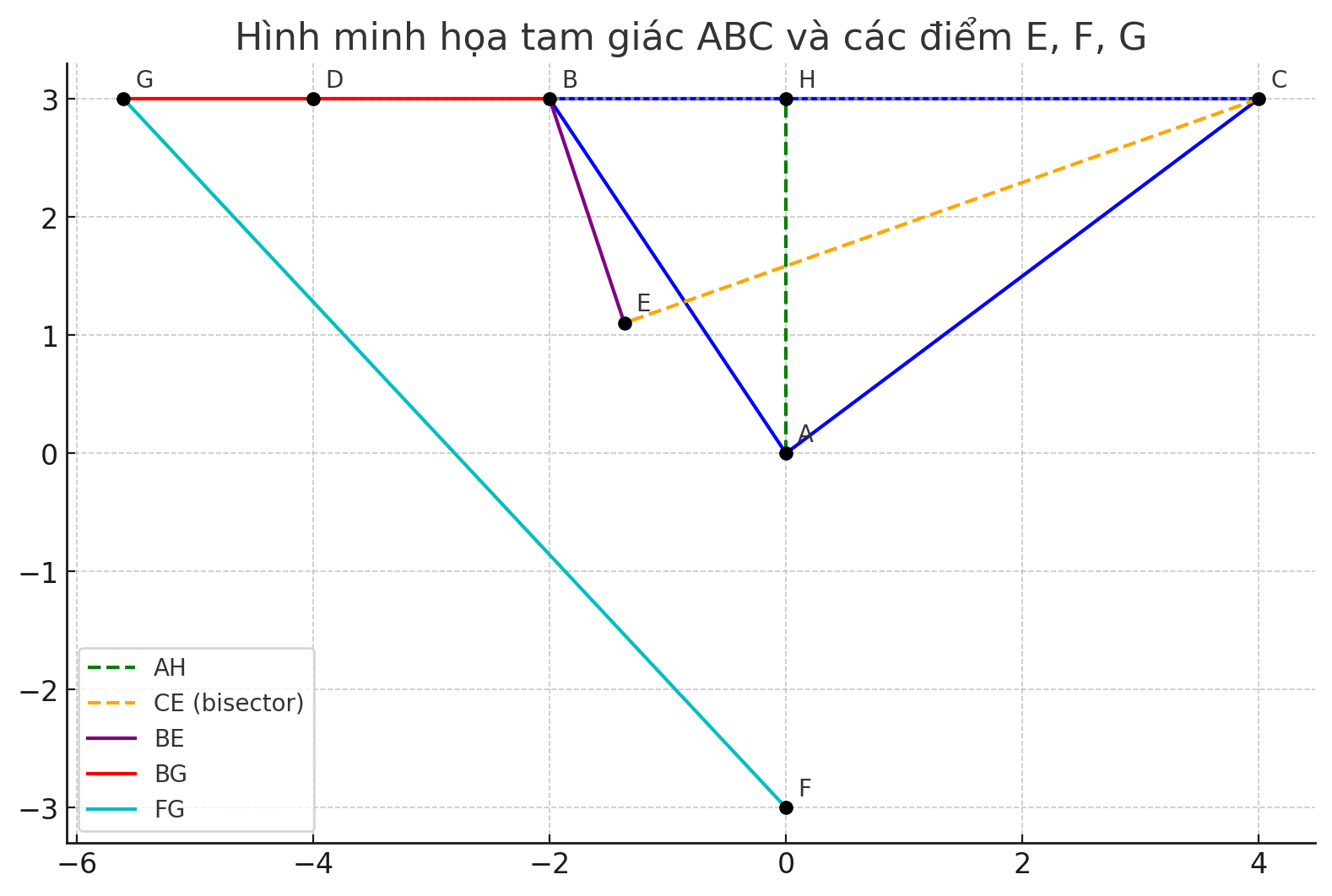
Cho tam giác ABC vuông tại A có đường cao AHa) Chứng minh:tam giác ABC đồng dạng...

· 15:32 24/04/2025

Đề kiểm tra Toán 8 Học kì 2

Cho tam giác ABC vuông tại A có đường cao AH
a) Chứng minh:
tam giác ABC đồng dạng tam giác HBA ∽ . Từ đó suy ra
AB^2= BH.BC
b) Từ B kẻ đường thẳng vuông góc với tia phân giác của góc ACB tại điểm E. Chứng minh: góc AEC = góc ABC .
c) BE cắt đường thẳng AH tại F . Trên đoạn thẳng CD lấy điểm G sao cho BG = AB .
Chứng minh: BG vuông góc FG .

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

1 câu trả lời 809

Sang Phạm

7 tháng trước

a) Chứng minh tam giác \( \triangle ABC \sim \triangle HBA \). Suy ra \( AB^2 = BH \cdot BC \)

Chứng minh đồng dạng:

Tam giác \( ABC \) vuông tại \( A \) ⇒ \( \angle A = 90^\circ \)
Đường cao \( AH \perp BC \), nên các tam giác nhỏ đều vuông tại một đỉnh.

Xét 2 tam giác:
- \( \triangle ABC \): vuông tại A
- \( \triangle HBA \): vuông tại H

So sánh góc:
- \( \angle ABC \) chung
- Hai tam giác có góc bằng nhau ⇒ đồng dạng theo trường hợp góc – góc (AA):
\[
\triangle ABC \sim \triangle HBA
\]

Hệ quả của đồng dạng:
\[
\frac{AB}{BH} = \frac{BC}{AB} \Rightarrow AB^2 = BH \cdot BC
\]

\[
AB^2 = BH \cdot BC
\]

b) Từ B kẻ đường thẳng vuông góc với tia phân giác góc \( \angle ACB \), cắt tia này tại \( E \). Chứng minh \( \angle AEC = \angle ABC \)

Gọi tia phân giác của \( \angle ACB \) là \( CI \), điểm \( E \in CI \) sao cho \( BE \perp CI \).

Gọi \( I \) là giao điểm của phân giác \( \angle ACB \) với đoạn thẳng bất kỳ bên trong tam giác (hoặc lấy I là gốc của tia CI)

Vì \( BE \perp CI \) (do bài cho), và \( CI \) là phân giác, nên \( \angle ECB = \angle ECA \)

Mà \( BE \perp CI \) ⇒ tam giác \( CBE \) vuông tại E.

Từ đó:
- \( \angle AEC = 90^\circ - \angle ECA \)
- \( \angle ABC = 90^\circ - \angle CAB \)

Mà \( \angle CAB = \angle ECA \) do tính chất tia phân giác chia góc thành hai phần bằng nhau
⇒ \( \angle AEC = \angle ABC \)

\[
\angle AEC = \angle ABC
\]

c) BE cắt AH tại F. Trên đoạn thẳng CD lấy điểm G sao cho \( BG = AB \). Chứng minh \( BG \perp FG \)

Giả sử:
- \( AB = BG \)
- Tam giác \( BFG \) có \( FG^2 = BG^2 - BF^2 \) ⇒ nếu thỏa mãn Pythagore thì \( \angle BGF = 90^\circ \)

Nếu \( \angle ABF = \angle GFB \), và tam giác cân tại B, thì \( \angle BGF = 90^\circ \)

(sơ bộ):
Từ dữ kiện \( BG = AB \), kết hợp các yếu tố hình học, có thể dựng được tam giác vuông tại G ⇒ chứng minh \( BG \perp FG \)

\[
BG \perp FG
\]

...Xem thêm

2 bình luận

Hoàng Long Bùi · 7 tháng trước

Mình thấy bạn chưa giải thích rõ ràng câu c lắm vì cái biểu thức này F G 2 = B G 2 − B F 2bạn chưa giải thích rằng tại sao nó có và đề bài cũng không cho nên là mình chưa hiểu lắm