a) Chứng minh tam giác \( ABD = \triangle AMD \)

Xét hai tam giác \( ABD \) và \( AMD \):
- \( AB = AM \)
- \( \angle ABD = \angle AMD \) (vì cùng chắn bởi phân giác \( AD \))
- Cạnh chung \( AD \)

⇒ Hai tam giác bằng nhau theo trường hợp cạnh – góc xen giữa – cạnh (c.g.c)

\[
\triangle ABD = \triangle AMD
\]

b) Tia \( MD \) cắt tia \( AB \) tại \( N \). Chứng minh \( \triangle BDN = \triangle MDC \)

Xét các tam giác \( BDN \) và \( MDC \):

Từ câu a, ta có:
- \( \triangle ABD = \triangle AMD \Rightarrow BD = MD \)

Trong tam giác:
- Có \( \angle DNB = \angle DCM \) (đối đỉnh hoặc dựng hình sẽ thấy bằng nhau)
- Cạnh \( BD = MD \)

⇒ Hai tam giác có:
- \( BD = MD \)
- Góc giữa hai cạnh tương ứng bằng nhau

⇒ Tam giác BDN = MDC theo trường hợp c.g.c

\[
\triangle BDN = \triangle MDC
\]

c) Chứng minh \( AD \) là đường trung trực của đoạn \( NC \)

Từ câu b):
- Hai tam giác \( BDN = MDC \)
⇒ \( DN = DC \) và \( \angle NDC = \angle MDC = \angle BDN \)

⇒ Từ đó suy ra tam giác \( NDC \) cân tại \( D \) và có \( AD \) đi qua đỉnh ứng với đáy \( NC \), đồng thời là phân giác

→ Nên \( AD \) là đường trung trực của \( NC \)

\[
AD \text{ là đường trung trực của } NC
\]

d) Chứng minh \( BD < DC \)

Từ giả thiết: \( AB < AC \)
→ Mà \( AM = AB \Rightarrow AM < AC \Rightarrow M \) nằm giữa \( A \) và \( C \)

Từ câu a: \( \triangle ABD = \triangle AMD \) ⇒ \( BD = MD \)

Từ hình: \( MD < DC \Rightarrow BD < DC \)

\[
BD < DC
\]

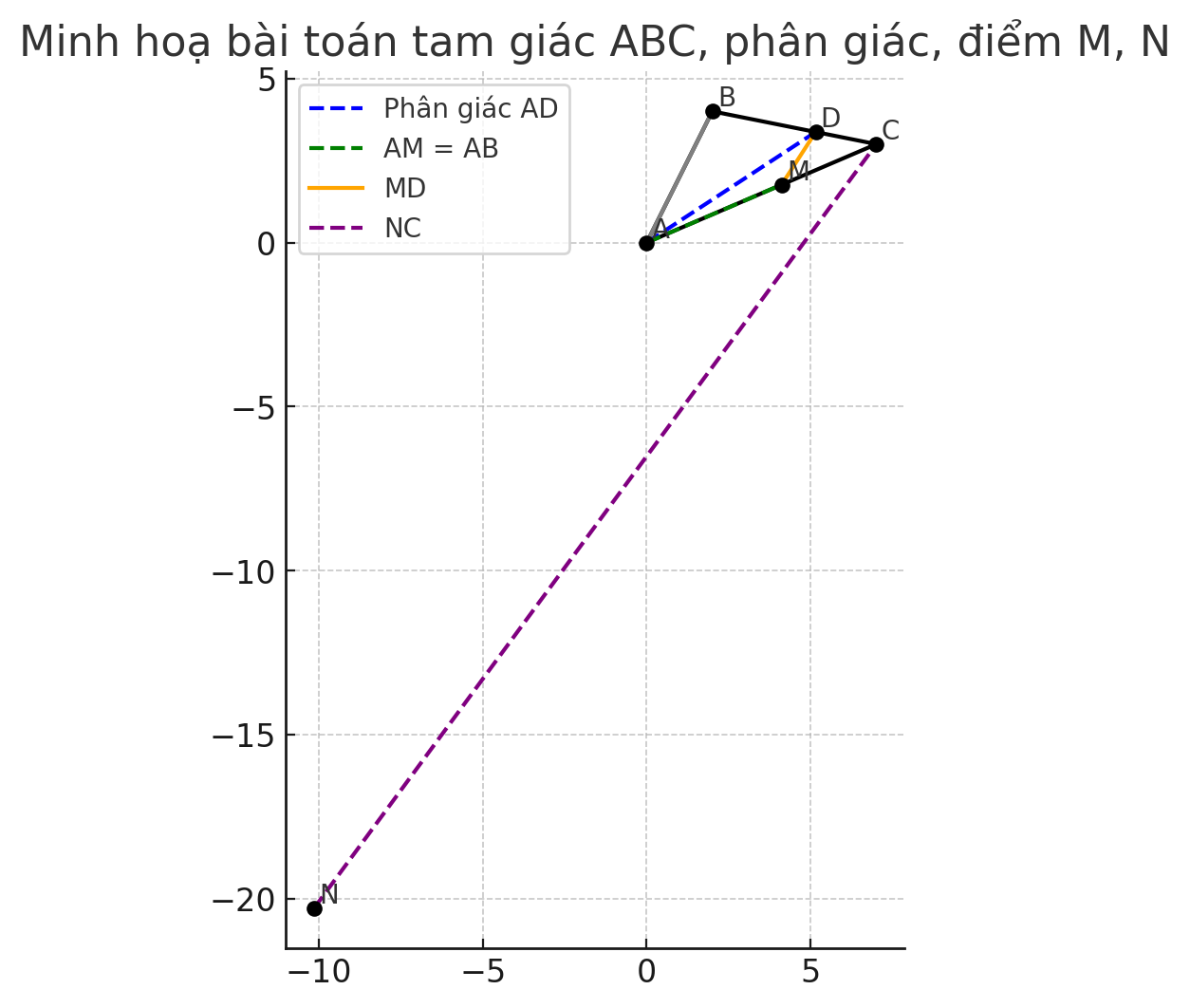
a) Xét ΔABD và ΔAMD:
AB = AM (gt)
∠BAD = ∠MAD (AD là phân giác)
AD chung
=> ΔABD = ΔAMD (c.g.c)

b) ΔABD = ΔAMD => ∠ABD = ∠AMD và BD = MD
Xét ΔBDN và ΔMDC:
∠DBN = ∠DMC (∠ABD = ∠AMD)
BD = MD
∠BDN = ∠MDC (đối đỉnh)
=> ΔBDN = ΔMDC (g.c.g)

c) ΔBDN = ΔMDC => BN = MC và DN = DC
AB + BN = AN và AM + MC = AC
Mà AB = AM và BN = MC => AN = AC
Xét ΔAND và ΔACD:
AN = AC
∠NAD = ∠CAD (AD là phân giác)
AD chung
=> ΔAND = ΔACD (c.g.c)
=> DN = DC và ∠ADN = ∠ADC
Vì ∠ADN = ∠ADC và DN = DC => AD là đường trung trực của NC.

d) Trong ΔABD, ∠ABD < 90 độ (tam giác ABC nhọn)
Mà ∠ABD = ∠AMD => ∠AMD < 90 độ
Trong ΔAMD, ∠AMD < 90 độ => ∠ADM > 90 độ
=> AD > BD (quan hệ góc cạnh trong tam giác)
Trong ΔADC, ∠ADC < 90 độ (∠ADC = ∠ADN và ∠ADN + ∠ADB = 180 độ, ∠ADB > 90 độ)
Mà ∠ADB > 90 độ => ∠ADC < ∠ADB
=> AC > AD (quan hệ góc cạnh trong tam giác)
Mà AD > BD => AC > BD
Lại có AC = AM + MC và AM = AB
=> AB + MC > BD
Mà MC = BN => AB + BN > BD
=> AN > BD
Vì AN = AC và AC = AM + MC = AB + BN
=> AB + BN = AN > BD + DN = DC + DN = DC + MC = DC + BN
Mà BN = MC => DC > BD
Vậy BD < DC.