Quảng cáo
2 câu trả lời 104
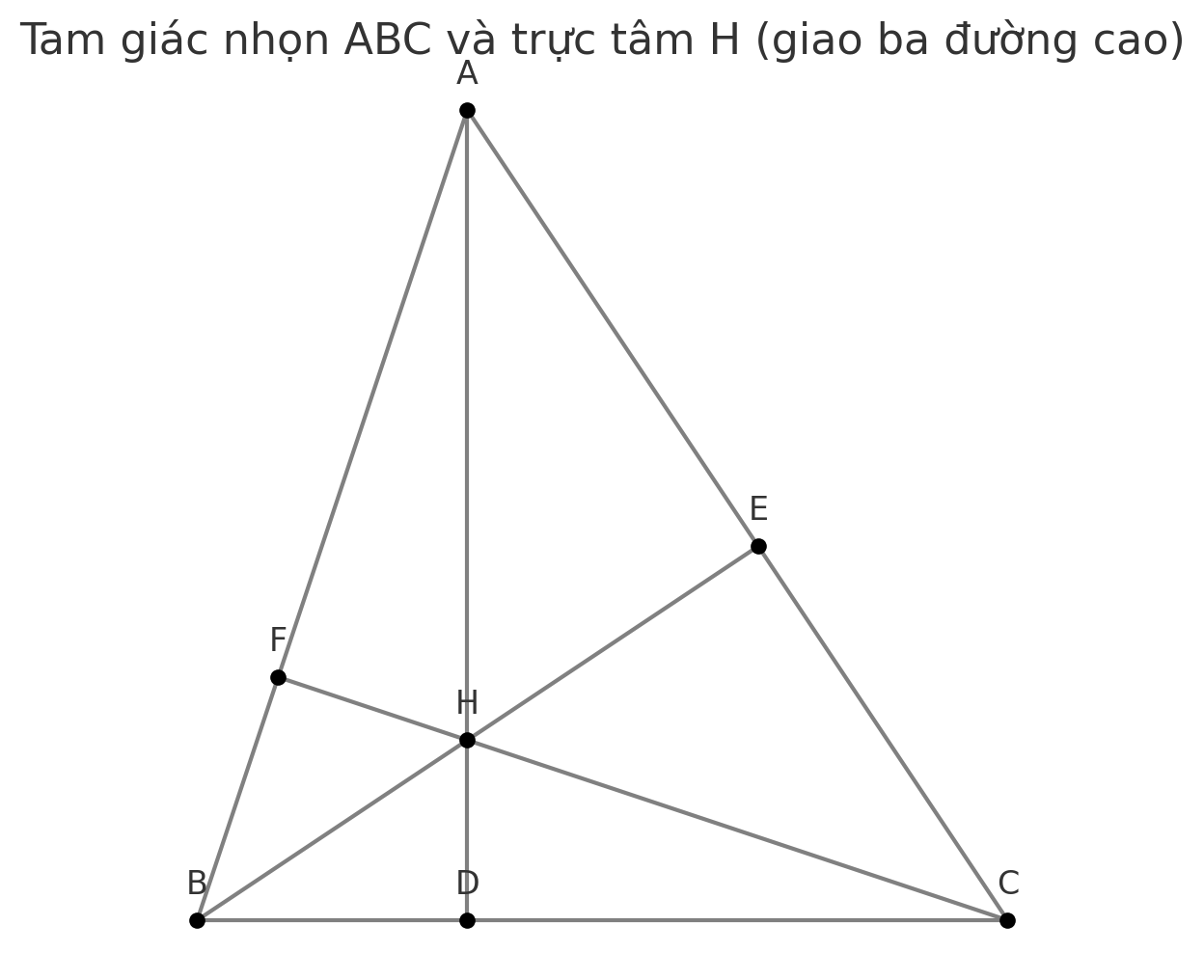
a) Xác định trực tâm của tam giác BHC
Các đường cao của tam giác BHC:
- Trong tam giác BHC:
- Đường cao từ B là BE (vì vuông góc với AC → nằm trong tam giác BHC)
- Đường cao từ C là CF (vuông góc với AB → nằm trong tam giác BHC)
- Đường cao từ H là đường nối H với A, vuông góc với BC → chính là đường cao AD
→ Ba đường cao trong tam giác BHC là:
- BE, CF, và AD
⇒ Ba đường cao đồng quy tại A
⇒ A là trực tâm của tam giác BHC
b) Xác định trực tâm của các tam giác phụ
Tam giác HAB:
- Trong tam giác HAB:
- CF là đường cao từ H (vuông góc với AB)
- AD là đường cao từ A (vuông góc với BC)
- BE là đường cao từ B (vuông góc với AC)
Ba đường này giao nhau tại điểm C
C là trực tâm của tam giác HAB
Tam giác HAC:
- Tương tự:
- AD: đường cao từ A (vuông góc với BC)
- BE: đường cao từ H (vuông góc với AC)
- CF: đường cao từ C (vuông góc với AB)
Ba đường này giao nhau tại điểm B
⇒ B là trực tâm của tam giác HAC
a) Tam giác HBC có HD, BE, CF là các đường cao. Trực tâm của tam giác HBC là A.
b) Tam giác HAB có HD, BF là các đường cao. Đường cao còn lại là AE. Trực tâm của tam giác HAB là C.
Tam giác HAC có HE, AF là các đường cao. Đường cao còn lại là BD. Trực tâm của tam giác HAC là B.
Quảng cáo
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK112000
-
78256
-
56023








