Quảng cáo
2 câu trả lời 320
Xét vectơ:
Ta phân tích:
\[
\vec{IF} = \vec{IG} + \vec{GE} + \vec{EF}
\]
Nhưng ta không cần đi vòng vậy, mà xét trực tiếp mối liên hệ giữa \( \vec{EG} \) và \( \vec{IF} \:
- \( \vec{EG} = \vec{EM} + \vec{MG} \)
- \( \vec{EM} = \frac{1}{2} \vec{EF} \)
- \( \vec{MG} = \frac{2}{3} \vec{MD} \)
Mà:
- \( \vec{IF} = \vec{IM} + \vec{MF} \)
- \( \vec{IM} = -\vec{MI} = -\vec{MG} = -\frac{2}{3} \vec{MD} \)
- \( \vec{MF} = \frac{1}{2} \vec{FE} = -\frac{1}{2} \vec{EF} \)
⇒
\[
\vec{IF} = -\frac{2}{3} \vec{MD} - \frac{1}{2} \vec{EF}
\Rightarrow -\vec{IF} = \frac{2}{3} \vec{MD} + \frac{1}{2} \vec{EF}
\Rightarrow \vec{EG} = -\vec{IF}
\]
\[
\vec{EG} = -\vec{IF} \Rightarrow EG \parallel IF
\]
(vì hai vectơ cùng phương, ngược hướng)
Đáp án: Đã chứng minh được \( \boxed{EG \parallel IF} \).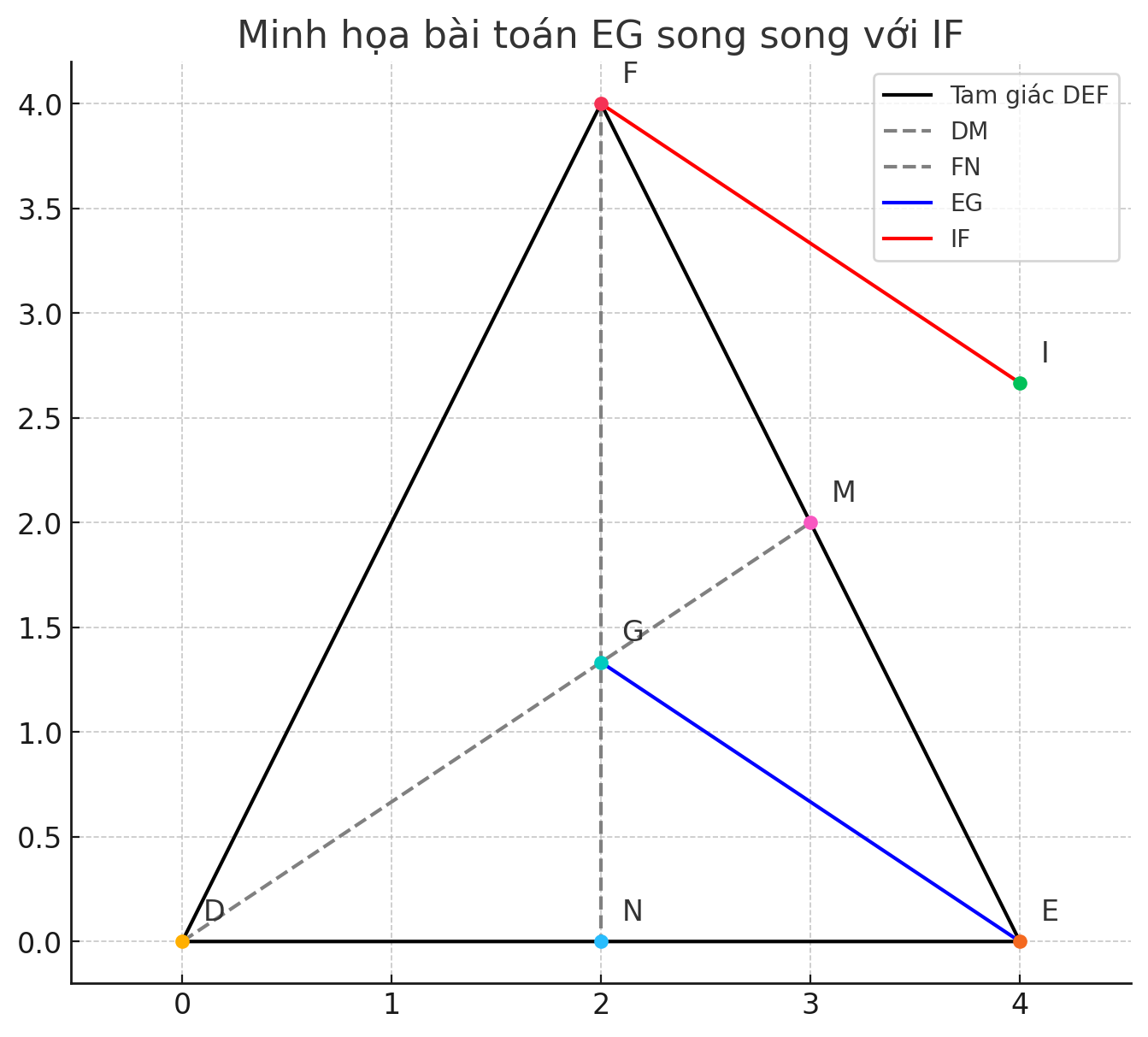
Chào bạn! Để chứng minh EG song song với IF trong tam giác DEF với các điều kiện đã cho, chúng ta sẽ sử dụng kiến thức về tính chất đường trung tuyến và hình bình hành. Dưới đây là các bước chứng minh chi tiết:
1. Xác định các điểm và đường thẳng:
Tam giác DEF có hai đường trung tuyến DM và FN cắt nhau tại G.
G là trọng tâm của tam giác DEF (vì là giao điểm của hai đường trung tuyến).
Trên tia đối của tia MD, lấy điểm I sao cho MI = MG.
2. Tính chất trọng tâm:
Trọng tâm G của tam giác chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn nối từ trọng tâm đến trung điểm cạnh đối diện.
Áp dụng cho đường trung tuyến DM, ta có: DG = 2GM.
Vì MI = MG (theo đề bài), suy ra DG = 2MI.
3. Xét tứ giác EIGF:
Chúng ta sẽ chứng minh tứ giác EIGF là hình bình hành. Nếu một tứ giác có các cặp cạnh đối song song hoặc các cặp cạnh đối bằng nhau hoặc các đường chéo cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình bình hành.
Xét đường chéo EF:
N là trung điểm của EF (vì FN là đường trung tuyến của tam giác DEF).
Xét đường chéo IG:
Theo cách dựng điểm I, M nằm giữa I và D, và MI = MG.
M là trung điểm của ID.
Điểm M là trung điểm của cả EF và ID:
M là trung điểm của EF (vì N là trung điểm EF và M nằm trên FN).
M là trung điểm của ID (theo cách dựng điểm I).
Kết luận về tứ giác EIGF:
Tứ giác EIGF có hai đường chéo EF và IG cắt nhau tại trung điểm M của mỗi đường.
Theo tính chất của hình bình hành, tứ giác EIGF là hình bình hành.
4. Chứng minh EG song song với IF:
Vì EIGF là hình bình hành (đã chứng minh ở bước 3), theo tính chất của hình bình hành, các cặp cạnh đối sẽ song song với nhau.
Do đó, EG song song với IF.
Vậy, chúng ta đã chứng minh được rằng EG song song với IF.
Tóm lại, mấu chốt của bài chứng minh này là việc xác định được điểm M là trung điểm của cả hai đường chéo EF và IG của tứ giác EIGF, từ đó suy ra tứ giác này là hình bình hành và dẫn đến kết luận EG song song với IF.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


