Cho tam giác tam giác ABC vuông tại A có AB = 6cm, BC = 10cm.
a. Tính độ dài cạnh AC và so sánh các góc của tam giác ABC.
b. Trên tia đối của AB lấy điểm D sao cho AD = AB. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AC tại M. Chứng minh BC = CD và tính độ dài đoạn thẳng AM.
c. Đường trung trực d của đoạn thẳng AC cắt đường thẳng DC tại Q. Chứng minh ba điểm B,M,Q thẳng hàng.
Quảng cáo
1 câu trả lời 6975
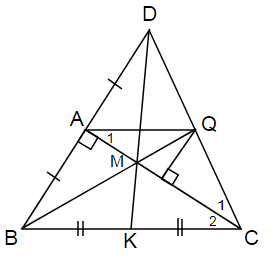
a) Xét △ABC vuông tại A có :
AB^2+AC^2=BC^2(định lý py-ta-go)
⇒ AC^2=BC^2-AB^2
⇒ AC^2=10^2-6^2
⇒ AC^2=100-36
⇒ AC^2=64
⇒ AC=8
Vậy AC=8cm
b)
Xét △ABC và △ADC có :
AC chung
AB=AD(gt)
∠BAC=∠DAC(=90)
⇒△ABC=△ADC(c-g-c)
⇒BC=DC(2 cạnh tương ứng)
Xét △BCD có BC=DC(cmt)
⇒△BCD cân tại C (định lý tam giác cân)
c)
Xét △BCD cân tại C có
K là trung điểm của BC (gt)
A là trung điểm của BD (gt)
⇒DK , AC là đường trung tuyến của △BCD
mà DK cắt AC tại M nên M là trọng tâm của △BCD
⇒CM=2/3AC
⇒CM=2/3.8
⇒CM=16/3cm
d)
Xét △AMQ và △CMQ có
MQ chung
MA=MC(gt)
∠AMQ=∠CMQ(=90)
⇒△AMQ=△CMQ(C-G-C)
⇒∠MAQ=∠C2(2 góc tương ứng )
QA=QC( 2 cạnh tương ứng)
Vì △ABC=△ADC(theo b)
⇒∠C1=∠C2(2 góc tương ứng)
⇒∠C1=∠MAQ
mà 2 góc này có vị trí SLT
⇒AQ//BC
⇒∠QAD=∠CBA( đồng vị )
mà∠CBA=∠CDA(△BDC cân tại C)
⇒∠QAD=∠QDA
⇒△ADQ cân tại Q
⇒QA=QD
mà QA=QC(cmt)
⇒DQ=CQ
⇒BQ là đường trung tuyến của△BCD
⇒B,M,D thẳng hàng
Quảng cáo
Câu hỏi hot cùng chủ đề
-
5445
Bài viết mới nhất Lớp 7
-
1 năm trước2147
