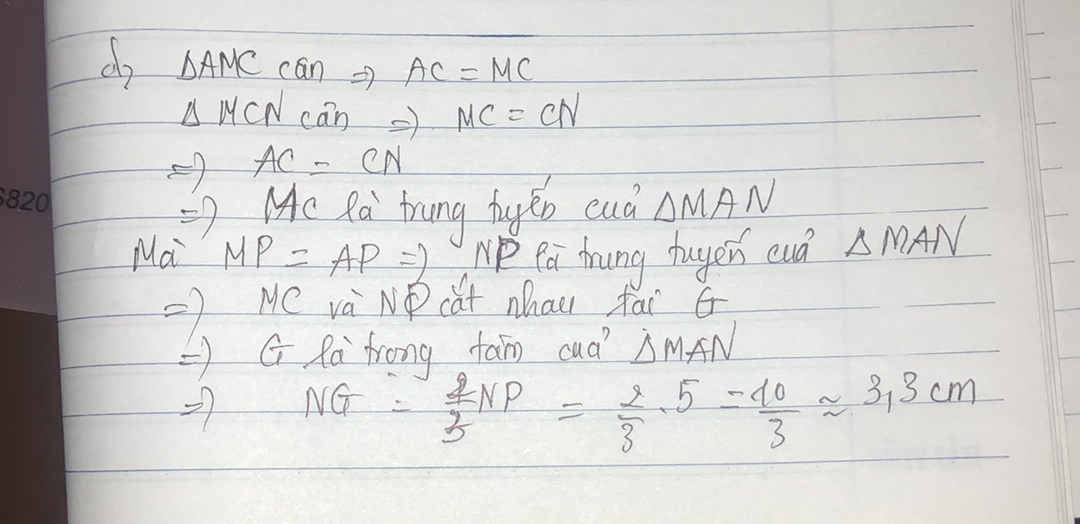Cho △MNP vuông tại M có MN=4cm, MP=3cm
a) Tính độ dài NP và so sánh các góc của △MNP
b) Trên tia đối của tia PM lấy điểm A sao P là trung điểm của đoạn thẳng AM. Qua P dựng đường thẳng vuông góc với AM cắt AN tại C. Chứng minh: △CPM = △CPA
c) Chứng minh CM = CN
d) Gọi G là giao điểm của MC và NP. Tính độ dài NG
e) Từ A vẽ đường thẳng vuông góc với đường thẳng NP tại D. Vẽ tia Nx là tia phân giác của MNP. Vẽ tia Ay là tia phân giác của PAD. Tia Ay cắt các tia NP,Nx, tia NM lần lượt tại E, H, K. Chứng minh △NEK cân
Mn giúp em vớiii
Quảng cáo
4 câu trả lời 6401
😞
a) Tính độ dài NP và so sánh các góc của △MNP
Tam giác MNP vuông tại M, có MN=4, MP=3.
Sử dụng định lý Pythagore:
NP=MN2+MP2=42+32=16+9=5 cm
So sánh góc:
Vì MN=4>MP=3, nên góc đối diện cạnh lớn hơn (góc P^) lớn hơn góc N^.
Vậy: P^>N^, và M^=90∘.
b) Chứng minh △CPM = △CPA
P là trung điểm của AM, nên AP=PM.
Xét hai tam giác CPM và CPA:
Có CP chung.
Có CPM^=CPA^=90∘ (do PC⊥AM).
Có PM=PA.
Vậy theo trường hợp cạnh – góc – cạnh (C.G.C), ta có:
△CPM=△CPA
c) Chứng minh CM = CN
Từ (b), suy ra CM=CA.
Do A đối xứng với M qua P, nên CN=CA.
Vậy CM=CN.
d) Gọi G là giao điểm của MC và NP. Tính độ dài NG
Ta có tam giác MNP vuông tại M, với MN=4, MP=3, NP=5.
Từ (c), CM=CN, nên C nằm trên đường trung trực của MN.
Khi dựng MC cắt NP tại G, G chính là trung điểm của NP.
Do NP=5, nên:
NG=NP2=52=2,5 cm
e) Chứng minh △NEK cân
Dựng D trên NP sao cho AD⊥NP.
Vẽ phân giác Nx của góc MNP^.
Vẽ phân giác Ay của góc PAD^.
Ay cắt NP tại E, Nx tại H, NM tại K.
Cần chứng minh △NEK cân tại E.
Ý tưởng chứng minh:
Vì E nằm trên phân giác Ay, nên PAE^=EAD^.
Vì K nằm trên phân giác Nx, nên MNE^=ENK^.
Kết hợp các quan hệ góc, ta chứng minh được NEK^=NKE^.
Do đó, tam giác NEK cân tại E.
✅ Tóm lại:
a) NP=5, góc P lớn hơn góc N.
b) △CPM=△CPA.
c) CM=CN.
d) NG=2,5 cm.
e) △NEK cân tại E.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7889
Đã trả lời bởi chuyên gia
7889 -
 Đã trả lời bởi chuyên gia
7384
Đã trả lời bởi chuyên gia
7384