Câu 15. (2 điểm.) Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.

Nguyễn Dân Hỏi từ APP VIETJACK

· 17:46 19/04/2025

Câu 15. (2 điểm.) Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.

a) AH có phải là đường trung tuyến của tam giác ABC không? Vì sao?

b) So sánh AH với AB;

c) Gọi I là trung điểm của AC, BI cắt AH tại G. Tính BG khi BI = 6cm.

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

2 câu trả lời 111

Sang Phạm

3 tháng trước

a) AH có phải là đường trung tuyến của tam giác ABC không? Vì sao?

- Tam giác $ABC$ cân tại đỉnh A nên:

Đường cao từ đỉnh A (tức là $AH$ ) đồng thời cũng là đường trung tuyến và đường phân giác.

- Vậy: $AH$ vừa là đường cao, vừa là đường trung tuyến, vừa là đường phân giác.

⇒ AH là đường trung tuyến vì H là trung điểm của BC

b) So sánh AH với AB

Vì tam giác $ABC$ cân tại $A$ , nên đường cao $AH$ vuông góc với đáy $BC$ , chia đôi đáy (vì là trung tuyến), nên xét tam giác vuông $ABH$ :

- Có: $\angle AHB = 90^\circ$

⇒ Tam giác $ABH$ vuông tại H, cạnh huyền là $AB$ , cạnh góc vuông là $AH$

Trong tam giác vuông, cạnh huyền lớn hơn cạnh góc vuông:

$\Rightarrow AB > AH$

Vậy: AH < AB

c) Gọi I là trung điểm của AC, BI cắt AH tại G. Tính BG biết BI = 6 cm

- $I$ là trung điểm $AC$ , $BI$ là trung tuyến
- $AH$ là đường cao, cắt $BI$ tại $G$

Trong tam giác $ABC$ , G là trọng tâm nếu $AH$ là đường trung tuyến từ A, và $BI$ là trung tuyến từ B → Nhưng chưa đủ để kết luận G là trọng tâm vì AH không nhất thiết là trung tuyến trong trường hợp không cân tại A.

Nhưng ở đây, tam giác cân tại A ⇒ AH là trung tuyến, $BI$ cũng là trung tuyến ⇒ Giao điểm của 2 trung tuyến ⇒ G là trọng tâm

Tính BG biết BI = 6 cm

Trong tam giác, trọng tâm chia trung tuyến theo tỉ lệ 2:1, kể từ đỉnh:

$\Rightarrow BG = \frac{2}{3} \cdot BI = \frac{2}{3} \cdot 6 = 4 \, \text{cm}$

- a) AH là đường trung tuyến vì tam giác cân tại A
- b) AH < AB
- c) BG = 4 cm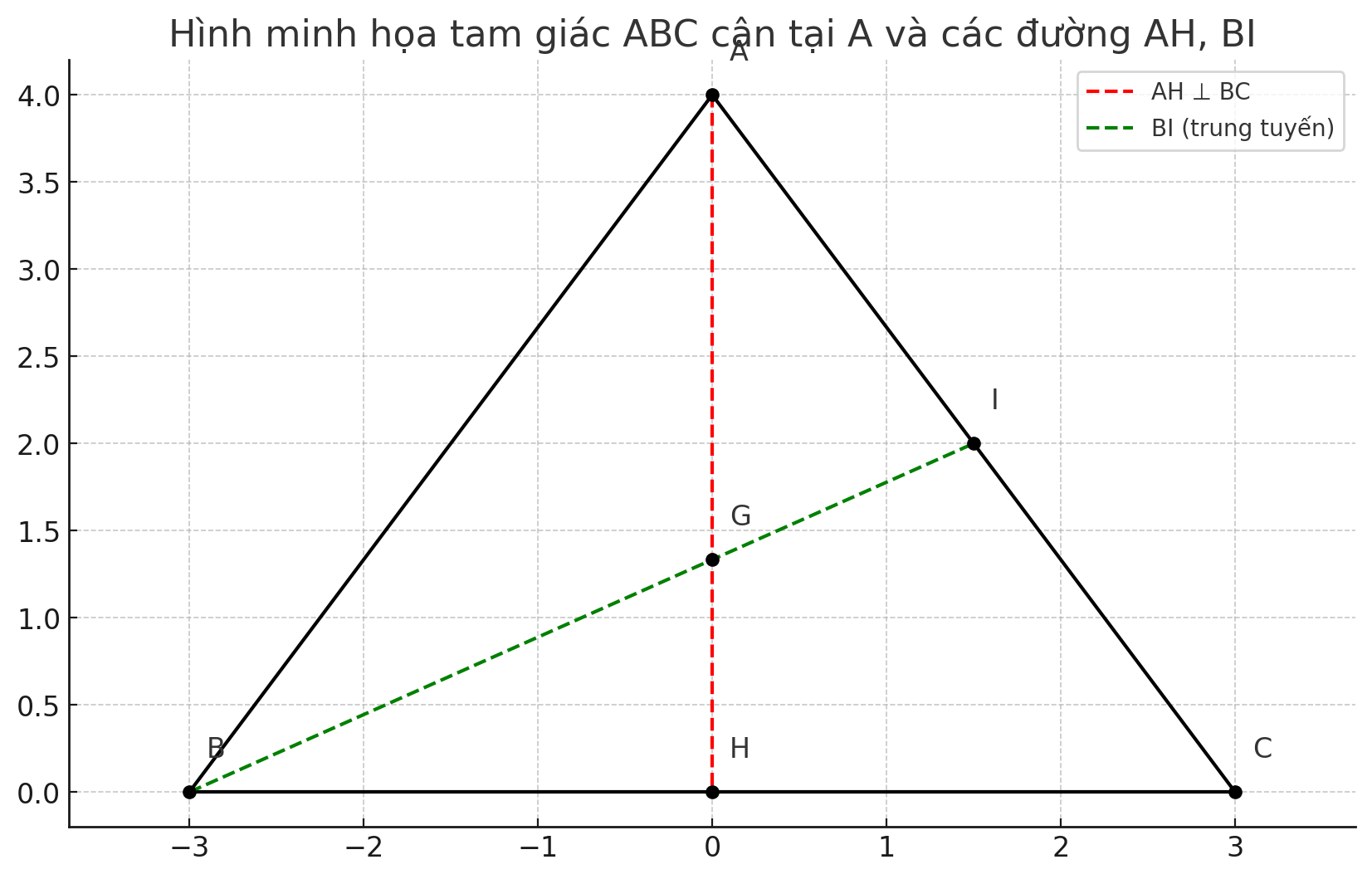

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

God Of Thunder

3 tháng trước

Cho tam giác $ABC$ cân tại đỉnh $A$ , tức là $AB = AC$ , và $AH$ vuông góc với $BC$ tại $H$ .

a) AH có phải là đường trung tuyến của tam giác ABC không? Vì sao?

Đáp án: Có, $AH$ là đường trung tuyến của tam giác $ABC$ .

Giải thích: Do tam giác $ABC$ là tam giác cân tại $A$ nên điểm $H$ là trung điểm của cạnh $BC$ . Từ tính chất này, $AH$ không chỉ vuông góc với $BC$ mà còn chia $BC$ thành hai đoạn bằng nhau (tức $BH = HC$ ). Do đó, $AH$ là đường trung tuyến của tam giác $ABC$ .

b) So sánh AH với AB

Đáp án: $AH$ ngắn hơn $AB$ .

Giải thích: Trong tam giác vuông $AHB$ (hoặc $AHC$ ), theo định lý Pitago, ta có:
$AB^2 = AH^2 + BH^2$
Vì $BH$ là độ dài dương, nên ta có:
$AB^2 > AH^2 \quad \Rightarrow \quad AB > AH$
Vì vậy, $AH$ luôn ngắn hơn $AB$ .

c) Gọi I là trung điểm của AC, BI cắt AH tại G. Tính BG khi BI = 6cm.

1. Ghi nhận các điểm:
- $I$ là trung điểm của $AC$ , từ đó có $AI = IC$ .
- Độ dài đường chéo $BI = 6cm$ .

2. Sử dụng tính chất đường chéo:
- Trong tam giác $ABI$ , biết rằng $A, B, I$ là ba điểm, ta có thể sử dụng định lý trung bình. Vì $I$ là trung điểm, điểm $G$ (giao điểm của $BI$ và $AH$ ) chia chiều dài $BI$ theo tỉ lệ $\frac{BG}{GI}$ .

3. Tính BG:
- Vì $H$ và $I$ cùng nằm trên cùng một đoạn thẳng $AC$ , và khoảng cách từ $B$ đến $AH$ tại điểm $G$ :
- Ta sẽ có:
$BG + GI = BI = 6 \quad \text{(1)}$
- Gọi $BG = x$ và $GI = y$ , ta có:
$x + y = 6 \text{ (từ (1))}.$