Question

Đã trả lời bởi chuyên gia

Answer 1

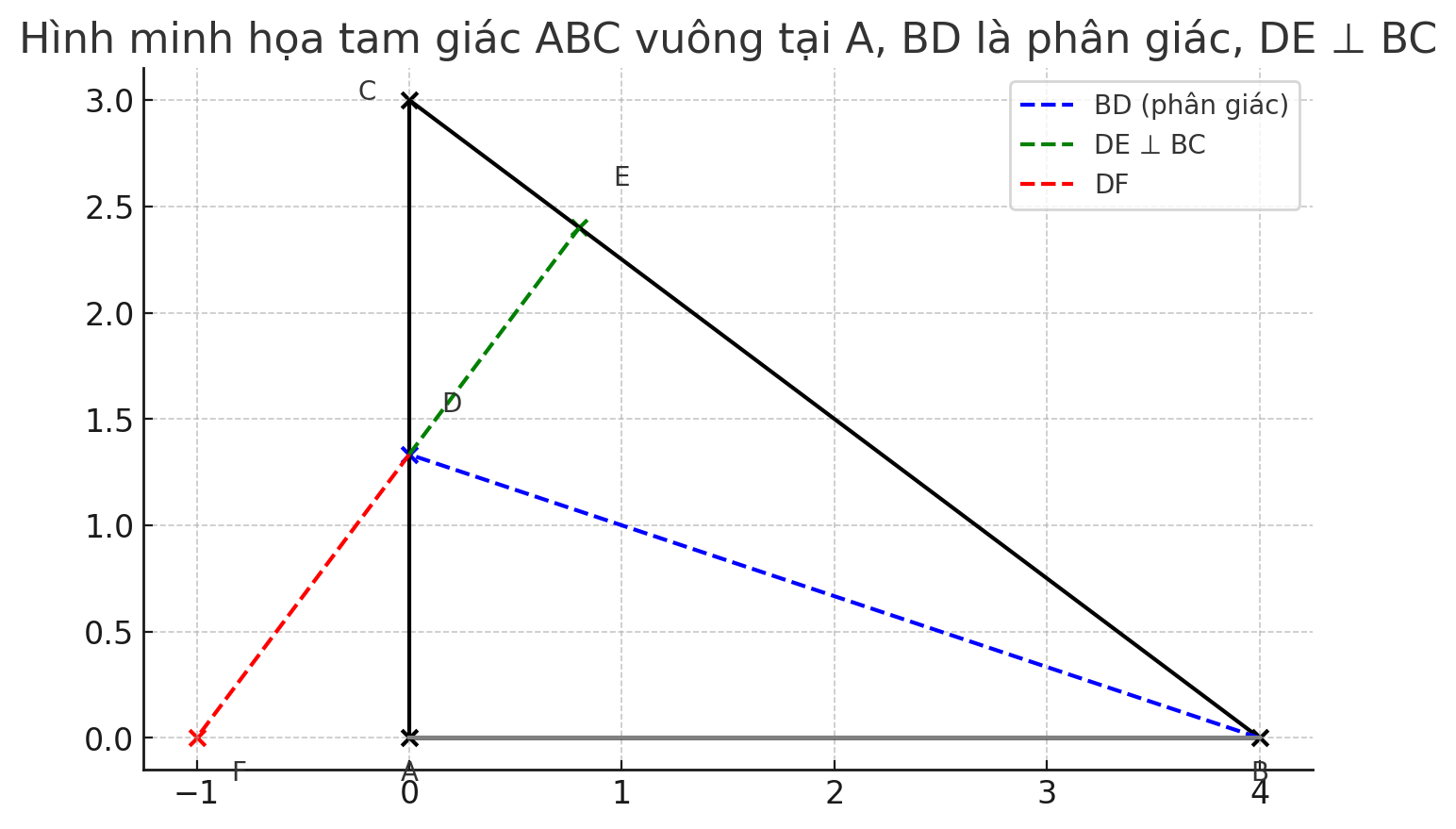
a. Chứng minh: DA = DE
b. Gọi ED cắt AB tại F. Chứng minh tam giác EDC cân tại D rồi suy ra DF > DE

a. Chứng minh: DA = DE

Xét tam giác ABD và tam giác EDB:

- DA và DE là hai đoạn cùng xuất phát từ D
- Góc ABD = EBD vì BD là phân giác của góc ABC
- DE ⊥ BC ⇒ góc DEB = 90°
- Tam giác ABC vuông tại A ⇒ góc DAB = 90° (vì A nằm trên AB vuông góc với AC, nên BD phân giác chia đôi góc vuông)

=> Hai tam giác DAB và DEB đều có một góc vuông và chung góc tại B ⇒ Chúng bằng nhau theo góc – góc (G-G) ⇒ DA = DE

DA = DE

b. Gọi ED cắt AB tại F. Chứng minh tam giác EDC cân tại D rồi suy ra DF > DE

Xét tam giác EDC:

- DE ⊥ BC
- D thuộc AC
- Ta đã có DA = DE (đã chứng minh ở câu a)
- Mà D nằm trên đoạn AC ⇒ Tam giác EDC có DA = DE, tức là 2 cạnh bằng nhau

=> Tam giác EDC cân tại D---

Tiếp theo: Suy ra DF > DE

Vì tam giác EDC cân tại D nên đường cao từ D (là DE) cũng là đường trung tuyến và phân giác ⇒ DE vuông góc và ngắn nhất trong các đoạn nối từ D đến các cạnh tam giác

Mà F nằm trên AB, nên DF nghiêng hơn DE ⇒ DF > DE

- a) DA = DE
- b) Tam giác EDC cân tại D ⇒ DF > DE

...Xem thêm

Answer 2