Góc giữa hai mặt phẳng (SBC) và (ABC) là góc giữa đường thẳng SA và hình chiếu của SA lên (SBC)

Mà SA ⊥ đáy, nên hình chiếu của SA lên mặt (SBC) chính là đường vuông góc kẻ từ A đến mặt phẳng (SBC)

=> Góc giữa hai mặt phẳng (SBC) và (ABC) chính là góc giữa SA và mặt phẳng (SBC)

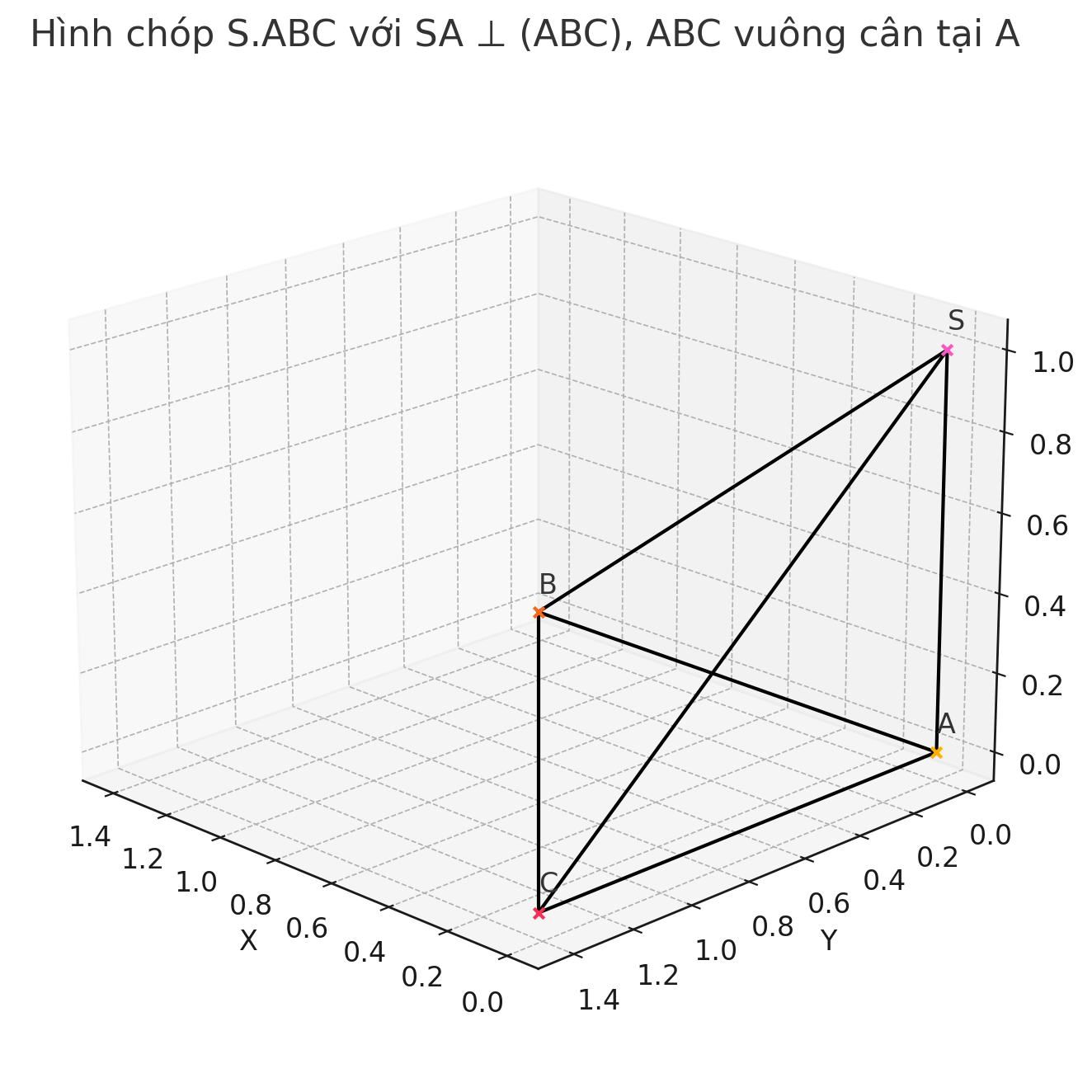
 Đặt hệ trục tọa độ:

Chọn:
- A(0; 0; 0)
- B(a√2; 0; 0)
- C(0; a√2; 0)
→ Vì tam giác ABC vuông cân tại A

⇒ SA = a → S(0; 0; a)

Tính góc giữa SA và mặt (SBC)

Ta tính góc giữa vector SA và mặt (SBC)
→ Dùng tích vô hướng giữa vector SA và vector pháp tuyến của (SBC)

Tính vector SA, SB, SC:

- SA = (0, 0, a)
- SB = (a√2, 0, –a)
- SC = (0, a√2, –a)

Tính vector pháp tuyến mặt (SBC):*

Lấy tích có hướng:
$\vec{n} = \vec{SB} \times \vec{SC}$

Tính:
$\vec{n} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a\sqrt{2} & 0 & -a \\ 0 & a\sqrt{2} & -a \\ \end{vmatrix} = \mathbf{i}(0 \cdot (-a) - a\sqrt{2} \cdot (-a)) - \mathbf{j}(a\sqrt{2} \cdot (-a) - 0 \cdot (-a)) + \mathbf{k}(a\sqrt{2} \cdot a\sqrt{2} - 0)$

$= \mathbf{i}(a^2\sqrt{2}) - \mathbf{j}(-a^2\sqrt{2}) + \mathbf{k}(2a^2) = (a^2\sqrt{2}, a^2\sqrt{2}, 2a^2)$

Tính cos(góc) giữa SA và mặt (SBC):

$\cos\theta = \frac{|\vec{SA} \cdot \vec{n}|}{\|\vec{SA}\| \cdot \|\vec{n}\|}$

- $\vec{SA} = (0, 0, a)$
- $\vec{n} = (a^2\sqrt{2}, a^2\sqrt{2}, 2a^2)$

Tính tích vô hướng:
$\vec{SA} \cdot \vec{n} = 0 + 0 + a \cdot 2a^2 = 2a^3$

Tính độ dài:
- $\|\vec{SA}\| = a$
- $\|\vec{n}\| = \sqrt{(a^2\sqrt{2})^2 + (a^2\sqrt{2})^2 + (2a^2)^2} = \sqrt{2a^4 + 2a^4 + 4a^4} = \sqrt{8a^4} = 2a^2\sqrt{2}$

Tính cosθ:

$\cos\theta = \frac{2a^3}{a \cdot 2a^2\sqrt{2}} = \frac{2a^3}{2a^3\sqrt{2}} = \frac{1}{\sqrt{2}} \Rightarrow \theta = \boxed{45^\circ}$

Góc giữa hai mặt phẳng (SBC) và (ABC) là $\boxed{45^\circ}$