Cho tam giác ABC cân tại A , kẻ AH vuông góc với canh BC tại H . Kẻ HM vuông góc AB tại M ; HN vuông góc AC tại N
a) Chừng minh: BH = CH
b) Chứng minh: tam giác AMN cân
Quảng cáo
3 câu trả lời 494
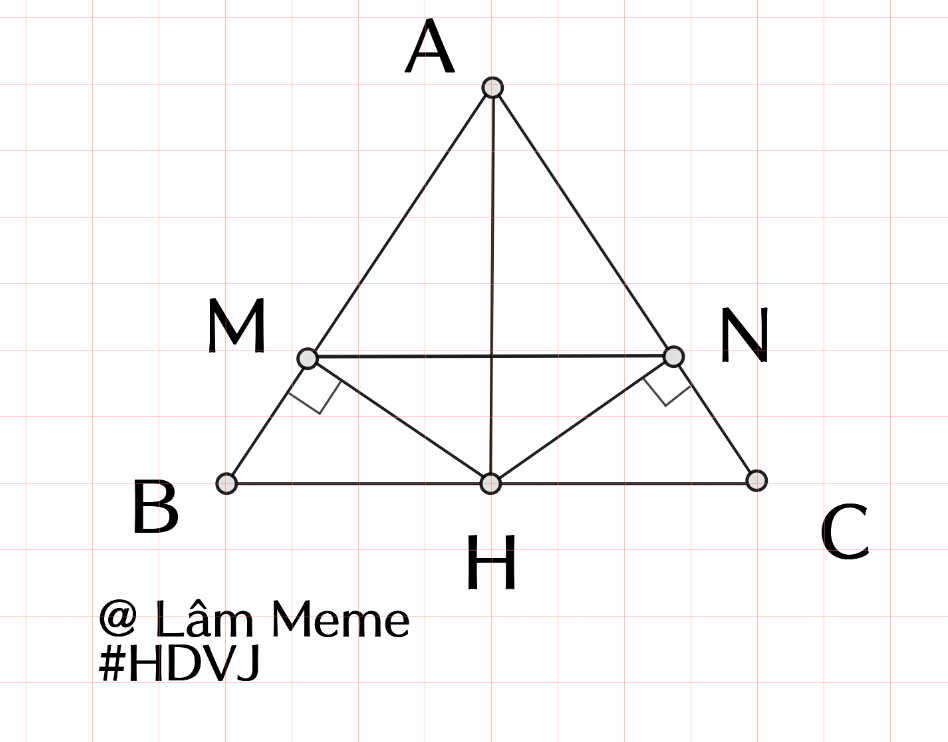
a) Xét `2` tam giác vuông: `triangleAHB` và `triangleAHC`
`AH` là cạnh chung
`AB=AC` (do `triangleABC` cân tại `A`)
`=>` `triangleAHB=triangleAHC` (cạnh huyền - cạnh góc vuông)
b) Xét `2` tam giác vuông: `triangleAHM` và `triangleAHN`
`AH` là cạnh chung
`hat{MAH}=hat{NAH}` (do `triangleABC` cân tại `A` có `AH` là đường cao đồng thời là phân giác)
`=>``triangleAHM=triangleAHN` (cạnh huyền - góc nhọn)
`=>` `AM=AN` (`2` cạnh tương ứng)
`=>` `triangleAMN` là tam giác cân (đpcm)
a) Xét 22 tam giác vuông: △AHB△AHB và △AHC△AHC
AHAH là cạnh chung
AB=ACAB=AC (do △ABC△ABC cân tại AA)
⇒⇒ △AHB=△AHC△AHB=△AHC (cạnh huyền - cạnh góc vuông)
b) Xét 22 tam giác vuông: △AHM△AHM và △AHN△AHN
AHAH là cạnh chung
ˆMAH=ˆNAHMAH^=NAH^ (do △ABC△ABC cân tại AA có AHAH là đường cao đồng thời là phân giác)
⇒⇒△AHM=△AHN△AHM=△AHN (cạnh huyền - góc nhọn)
⇒⇒ AM=ANAM=AN (22 cạnh tương ứng)
⇒⇒ △AMN△AMN là tam giác cân (đpcm
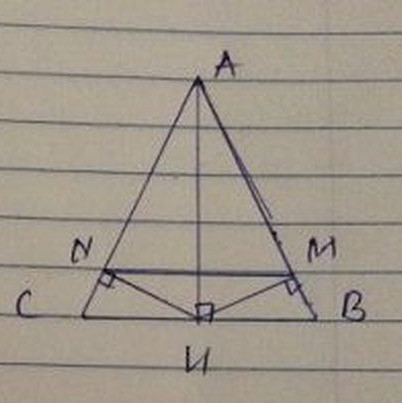
📐 Chứng minh các tính chất của tam giác cân
a) Chứng minh: BH = CH
Ta có $\triangle \mathbf{ABC}$ cân tại A.
Theo tính chất của tam giác cân, đường cao $\mathbf{AH}$ (kẻ từ đỉnh A và vuông góc với cạnh đáy BC) đồng thời là đường trung tuyến của tam giác đó.
Vì AH là đường trung tuyến của BC nên $\mathbf{H}$ là trung điểm của BC.
Do đó:
(Điều phải chứng minh)
b) Chứng minh: Tam giác AMN cân
Để chứng minh $\triangle AMN$ cân, ta cần chứng minh $\mathbf{AM = AN}$ hoặc $\widehat{AMN} = \widehat{ANM}$. Ta sẽ chứng minh $\mathbf{AM = AN}$.
Xét $\triangle \mathbf{AHB}$ vuông tại H (vì $AH \perp BC$) và $\triangle \mathbf{AHC}$ vuông tại H.
$AB = AC$ (do $\triangle ABC$ cân tại A)
$AH$ là cạnh chung.
$\widehat{B} = \widehat{C}$ (Góc đáy của tam giác cân).
Suy ra $\triangle AHB = \triangle AHC$ (Cạnh huyền - Cạnh góc vuông hoặc Cạnh huyền - Góc nhọn).
Do đó $\widehat{BAH} = \widehat{CAH}$. Hay $\mathbf{AH}$ là tia phân giác của $\widehat{BAC}$.
Ta có:
$HM \perp AB$ tại M $\implies$ HM là khoảng cách từ H đến AB.
$HN \perp AC$ tại N $\implies$ HN là khoảng cách từ H đến AC.
Vì $\mathbf{AH}$ là tia phân giác của $\widehat{BAC}$ (đã chứng minh ở trên), theo tính chất của tia phân giác, mọi điểm nằm trên tia phân giác cách đều hai cạnh của góc đó.
Điểm H nằm trên tia AH.
Suy ra $\mathbf{HM = HN}$.
Xét $\triangle \mathbf{AMH}$ vuông tại M ($HM \perp AB$) và $\triangle \mathbf{ANH}$ vuông tại N ($HN \perp AC$).
$\mathbf{AH}$ là cạnh huyền chung.
$\mathbf{HM = HN}$ (chứng minh ở trên).
Do đó $\triangle AMH = \triangle ANH$ (Cạnh huyền - Cạnh góc vuông).
Từ đó suy ra các cạnh tương ứng bằng nhau:
Vì $\triangle AMN$ có $\mathbf{AM = AN}$ nên $\triangle AMN$ là tam giác cân tại A.
(Điều phải chứng minh)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7813
Đã trả lời bởi chuyên gia
7813 -
 Đã trả lời bởi chuyên gia
7318
Đã trả lời bởi chuyên gia
7318 -
 Đã trả lời bởi chuyên gia
6311
Đã trả lời bởi chuyên gia
6311


