Cho tam giác ABC cân tại A Kẻ trung tuyến BM và CN (M thuộc AC, N thuộc AB) Chứng minh:BM=CN

Quy kim Hỏi từ APP VIETJACK

đã hỏi trong Lớp 7 Toán học

· 04:40 05/04/2025

Cho tam giác ABC cân tại A
Kẻ trung tuyến BM và CN (M thuộc AC, N thuộc AB)
Chứng minh:BM=CN

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

2 câu trả lời 113

Sang Phạm

4 tháng trước

Cần chứng minh: $BM = CN$

Ta sử dụng định lý trung tuyến trong tam giác:

Trong một tam giác, trung tuyến ứng với cạnh đối có độ dài xác định bởi công thức:

$\text{Trung tuyến từ đỉnh } B \text{ đến cạnh } AC: \quad BM^2 = \frac{1}{2}(AB^2 + BC^2) - \frac{1}{4}AC^2$

$\text{Trung tuyến từ đỉnh } C \text{ đến cạnh } AB: \quad CN^2 = \frac{1}{2}(AC^2 + BC^2) - \frac{1}{4}AB^2$

Nhưng vì tam giác cân tại $A$ , nên:
$AB = AC \Rightarrow AB^2 = AC^2$

⇒ Hai biểu thức trên trở thành:

$BM^2 = \frac{1}{2}(AB^2 + BC^2) - \frac{1}{4}AB^2$
$CN^2 = \frac{1}{2}(AB^2 + BC^2) - \frac{1}{4}AB^2$

⇒ $BM^2 = CN^2 \Rightarrow BM = CN$

$\boxed{BM = CN}$

(hai trung tuyến từ đỉnh B và C bằng nhau trong tam giác cân tại A)

0 bình luận

Đăng nhập để hỏi chi tiết

Ngọc

4 tháng trước

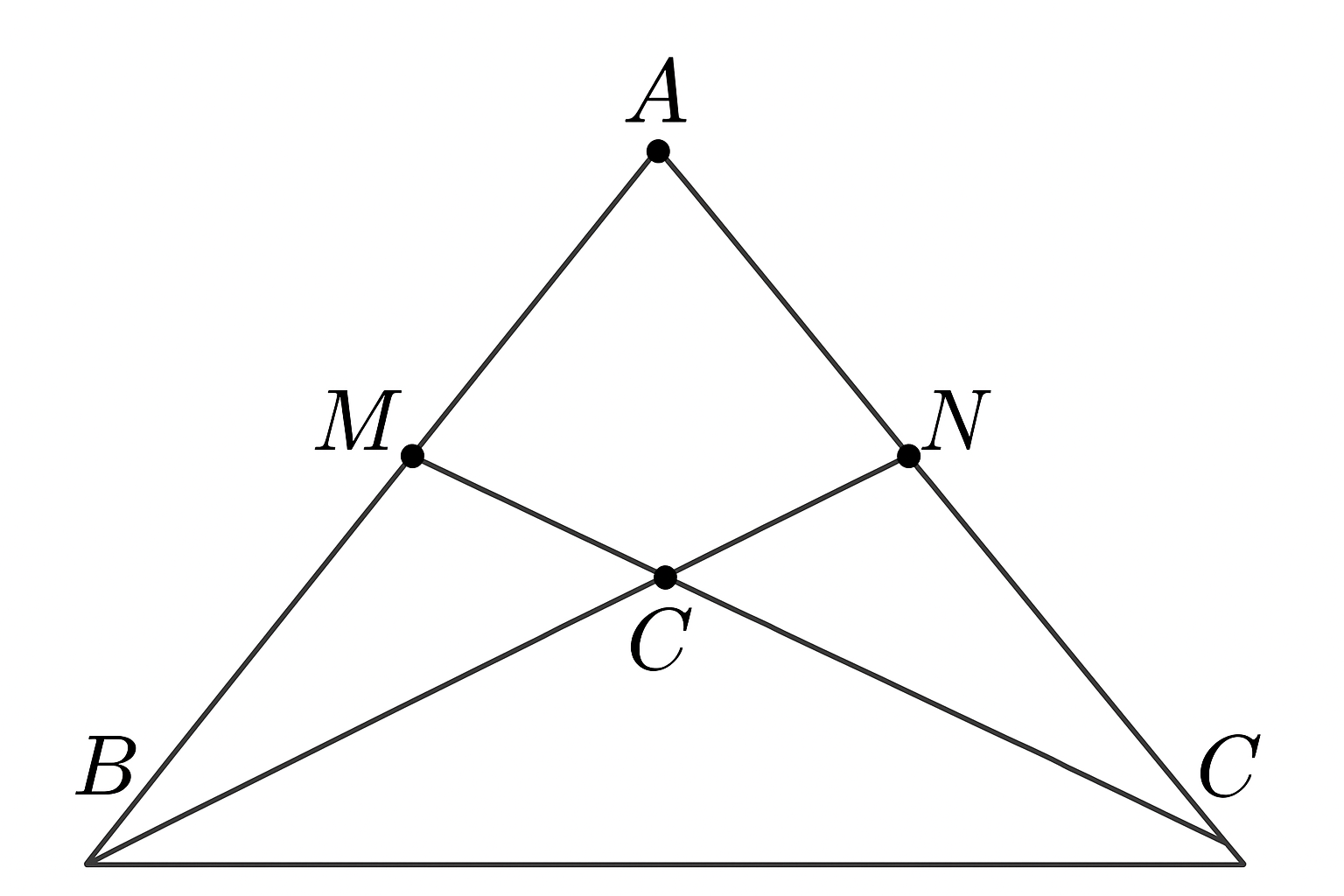
Giả thiết:

Tam giác ABC cân tại A.

BM là trung tuyến (M là trung điểm AC).

CN là trung tuyến (N là trung điểm AB).
=>

BM = CN.

Sử dụng trường hợp bằng nhau Cạnh - Góc - Cạnh

Vì tam giác ABC cân tại A:

AB = AC (Định nghĩa tam giác cân)

Góc ABC = Góc ACB (Tính chất tam giác cân)

Vì BM là trung tuyến: M là trung điểm của AC, nên AM = MC = AC / 2.
Vì CN là trung tuyến: N là trung điểm của AB, nên AN = NB = AB / 2.
Từ AB = AC (chứng minh trên), suy ra: AN = NB = AM = MC.

Xét hai tam giác ABM và ACN:

AB = AC (chứng minh trên)

Góc A là góc chung

AM = AN (chứng minh trên)

=> Tam giác ABM = Tam giác ACN (c.g.c)

Suy ra: BM = CN (Là hai cạnh tương ứng của hai tam giác bằng nhau).
hoặc em có thể dùng bằng nhau Cạnh - Góc - Cạnh cung duoc

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

2 câu trả lời 113

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 7