Quảng cáo
3 câu trả lời 432
Giao tuyến của hai mặt phẳng \( (SBC) \cap (SCD) = SC \)
→ Góc giữa hai mặt phẳng chính là góc giữa hai mặt phẳng bên cạnh giao tuyến \( SC \)
Chọn:
- Trong mặt \( SBC \): lấy đoạn \( SB \)
- Trong mặt \( SCD \): lấy đoạn \( SD \)
Cả hai đều xuất phát từ điểm chung \( S \)
Vậy: góc giữa hai mặt phẳng \( (SBC) \) và \( (SCD) \) chính là góc \( \angle BSD \)
Tính góc \( \angle BSD \):
Do \( ABCD \) là hình vuông ⇒ \( BD \) là đường chéo của hình vuông ⇒ \( BD \perp AC \)
- Tâm \( O \) là giao điểm hai đường chéo \( AC \) và \( BD \)
- \( SA \perp (ABCD) \) ⇒ \( SA \perp BD \), nên tam giác \( SBD \) là tam giác cân tại \( S \) nếu \( AB = a \)
Tính độ dài:
- \( AB = a \Rightarrow BD = a\sqrt{2} \)
- \( SA \perp mặt đáy \) ⇒ tam giác \( SAB, SAD, SBC, SCD \) đều là tam giác vuông
Giả sử chiều cao \( SA = h \), thì tam giác \( SBD \) có:
- \( SB^2 = h^2 + a^2 \)
- \( SD^2 = h^2 + a^2 \)
- \( BD = a\sqrt{2} \)
Áp dụng định lý cosin trong tam giác \( SBD \):
\[
\cos \angle BSD = \frac{SB^2 + SD^2 - BD^2}{2 \cdot SB \cdot SD}
\]
Thay số vào:
- \( SB^2 = SD^2 = h^2 + a^2 \)
- \( BD^2 = 2a^2 \)
\[
\cos \angle BSD = \frac{(h^2 + a^2) + (h^2 + a^2) - 2a^2}{2 \cdot \sqrt{h^2 + a^2} \cdot \sqrt{h^2 + a^2}} = \frac{2h^2}{2(h^2 + a^2)} = \frac{h^2}{h^2 + a^2}
\]
⇒ Góc giữa hai mặt phẳng là:
\[
\boxed{\angle BSD = \cos^{-1}\left(\frac{h^2}{h^2 + a^2}\right)}
\]
Góc giữa hai mặt phẳng \( (SBC) \) và \( (SCD) \) là góc \( \angle BSD \), với:
\[
\cos \angle BSD = \frac{h^2}{h^2 + a^2}
\]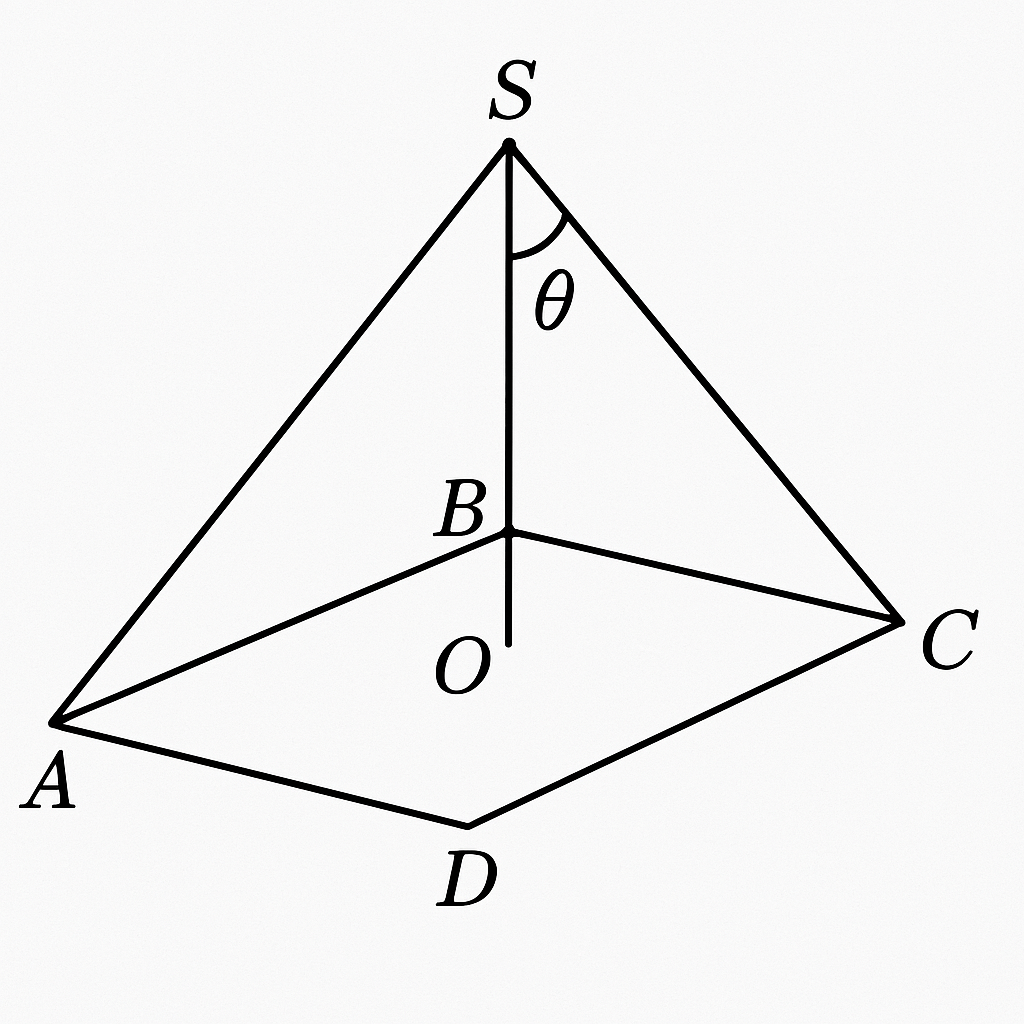
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy. Xét hai mặt phẳng (SBC) và (SCD), chúng có giao tuyến chung là SC. Góc giữa hai mặt phẳng này chính là góc giữa hai đường thẳng nằm trong hai mặt phẳng đó và cùng vuông góc với SC
Trong mặt phẳng đáy ABCD, do ABCD là hình vuông nên BC⊥CD. Vì vậy, góc giữa hai mặt phẳng (SBC) và (SCD) chính là góc giữa BC và CD, tức là 90∘.
Vậy góc giữa hai mặt phẳng (SBC) và (SCD) là:90∘.
Xác định giao tuyến
. Do đó, BC ⊥ SB. Vậy tam giác SBC vuông tại B.
Xét hai tam giác vuông SBC và SCD:
BD là đường chéo hình vuông nên BD = a√2.
Tam giác SBC vuông tại B, BH là đường cao:
SB = √(SA² + AB²) = √(h² + a²)
SC = √(SA² + AC²) = √(h² + (a√2)²) = √(h² + 2a²)
Hệ thức lượng trong tam giác vuông SBC: 1/BH² = 1/SB² + 1/BC² = 1/(h² + a²) + 1/a²
=> BH² = (a²(h² + a²)) / (h² + 2a²)
=> BH = (a√(h² + a²)) / √(h² + 2a²)
cos(∠BHD) = (2 * BH² - BD²) / (2 * BH²)
cos(∠BHD) = 1 - BD² / (2 * BH²)
cos(∠BHD) = 1 - (a√2)² / [ 2 * (a²(h² + a²)) / (h² + 2a²) ]
cos(∠BHD) = 1 - 2a² / [ (2a²(h² + a²)) / (h² + 2a²) ]
cos(∠BHD) = 1 - [ 2a² * (h² + 2a²) ] / [ 2a² * (h² + a²) ]
cos(∠BHD) = 1 - (h² + 2a²) / (h² + a²)
cos(∠BHD) = ( (h² + a²) - (h² + 2a²) ) / (h² + a²)
cos(∠BHD) = -a² / (h² + a²)
cos(∠BHD) = -a² / (h² + a²)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134901
Đã trả lời bởi chuyên gia
134901 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
76057
Đã trả lời bởi chuyên gia
76057 -
 Đã trả lời bởi chuyên gia
71711
Đã trả lời bởi chuyên gia
71711 -
 Đã trả lời bởi chuyên gia
47598
Đã trả lời bởi chuyên gia
47598


