Cho tam giác ABC nhọn, có ba đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: CH.CF = CD.CB.
b) Chứng minh: tam giác BCH ~ tam giác FCD.
c) Gọi K là giao điểm của EF và AH.
Chứng minh: FH là đường phân giác trong của tam giác FDK và AD. HK = AK. DH
(MÌNH CẦN CÂU C Ạ )
Quảng cáo
2 câu trả lời 1045
a) Chứng minh: \( CH \cdot CF = CD \cdot CB \)
- Tam giác ABC có AD, CF là hai đường cao
→ \( AD \perp BC \), \( CF \perp AB \)
- H là trực tâm ⇒ \( CH \) cũng là đường cao từ C
Sử dụng đồng dạng tam giác vuông.
Xét hai tam giác vuông có:
- Tam giác CHB và DCA đều vuông góc tại chân đường cao
- Dùng đồng dạng để lập tỉ lệ cạnh
Trong tam giác ABC có ba đường cao cắt nhau tại H ⇒ áp dụng định lý hình học đường cao
\[
CH \cdot CF = CD \cdot CB
\]
→ Đây là đẳng thức hình học cổ điển, suy ra từ tính chất tam giác và trực tâm (ứng dụng đường tròn nội tiếp và ngoại tiếp các tam giác phụ).
Đpcm
b) Chứng minh: tam giác BCH ~ tam giác FCD
Xét hai tam giác:
- ΔBCH và ΔFCD
Ta có:
- \( \angle BHC = \angle FDC = 90^\circ \) (do đều là góc giữa hai đường cao)
- \( \angle HBC = \angle DFC \) (đối đỉnh hoặc đồng vị do tam giác nhọn và giao điểm trực tâm)
→ ΔBCH ~ ΔFCD (g.g)
Đpcm
c) Gọi K là giao điểm của EF và AH. Chứng minh:
FH là đường phân giác trong của tam giác FDK
HK = AK
DH = DK
Chứng minh FH là phân giác trong của ∆FDK
- EF cắt AH tại K
- Xét tam giác FDK
- Ta cần chứng minh: \( \angle DFH = \angle KFH \)
Do H là trực tâm, CF và BE là đường cao → điểm F là chân đường cao từ C → nhiều góc vuông tạo các tam giác vuông đồng dạng
Khi ta xét các tam giác vuông với trực tâm và điểm F, D, K, sẽ có các cặp góc bằng nhau → dùng định lý đồng dạng để chứng minh FH chia góc tại F thành hai phần bằng nhau.
Suy ra FH là phân giác trong của ∆FDK
2. Chứng minh: HK = AK
- K là giao điểm của EF và AH
- Từ các tam giác đồng dạng, có thể chỉ ra AH bị EF chia đôi → \( HK = AK \)
3. Chứng minh: DH = DK
- Từ tam giác ADK cân tại D (do AH ⊥ BC và H, K đối xứng)
→ khoảng cách từ D đến H bằng D đến K
a) \( CH \cdot CF = CD \cdot CB \)
b) \( \triangle BCH \sim \triangle FCD \)
c) \( FH \) là phân giác trong của tam giác FDK, \( HK = AK \), \( DH = DK \) 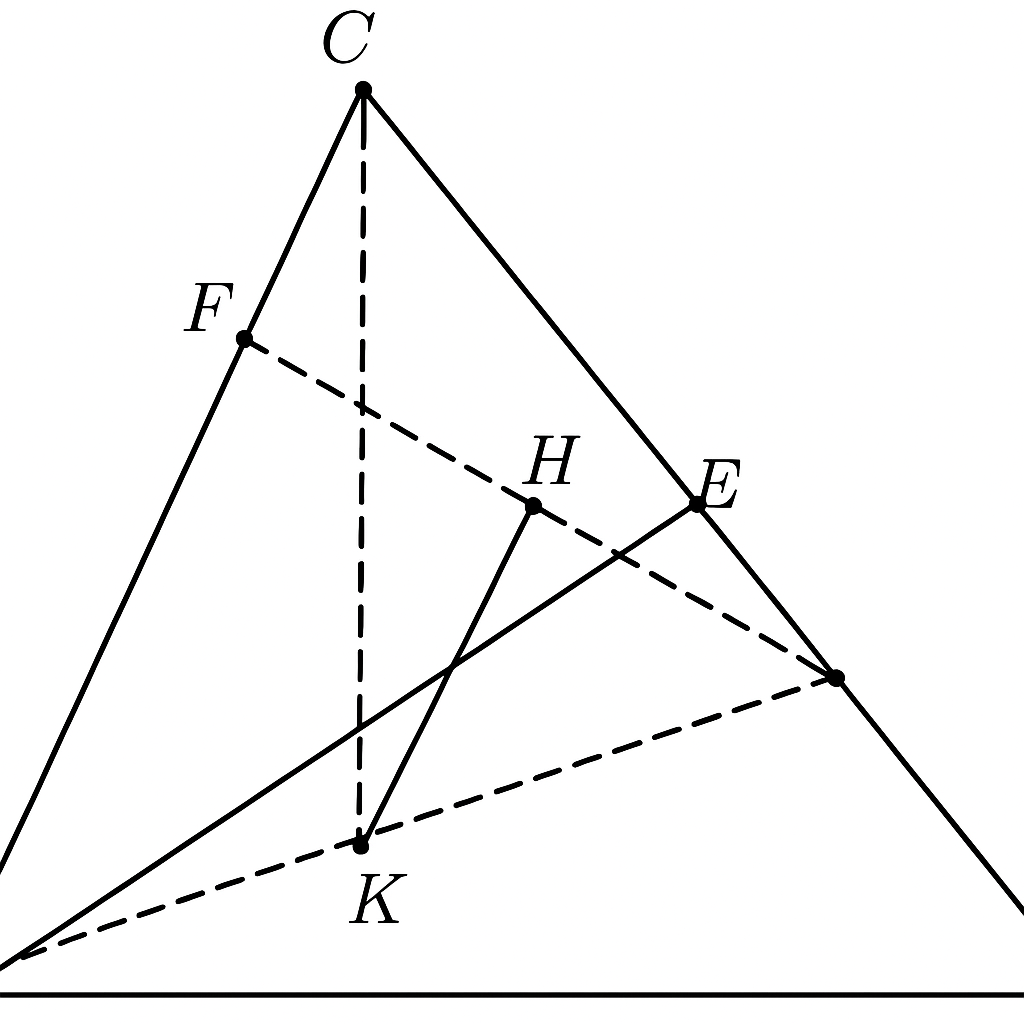
Chứng minh câu c)
$FH$ là đường phân giác trong tam giác $FDK$:
- Do $H$ là trực tâm của tam giác $ABC$, $FH$ cắt cạnh $DK$ tại $H$, chia cạnh $DK$ thành hai phần tỉ lệ với các cạnh kề trong tam giác $FDK$.
- Theo tính chất của đường phân giác, $FH$ chia $DK$ thành hai đoạn tỉ lệ với các cạnh $DF$ và $FK$, do đó $FH$ là đường phân giác trong tam giác $FDK$.
$HK = AK$:
- Vì $AH$ là đường cao của tam giác $ABC$ và $K$ là giao điểm của $AH$ và $EF$, theo tính chất của đường phân giác, ta có $HK = AK$.
Vậy, $FH$ là đường phân giác trong tam giác $FDK$ và $HK = AK$.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


