Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G
a) tính tỉ số BD/BG và CE/CG
b) chứng minh rằng BD+CE > BC
Quảng cáo
2 câu trả lời 876
a) Tính tỉ số
\( \dfrac{BD}{BG} \approx 1.5 \)
\( \dfrac{CE}{CG} \approx 1.5 \)
Đây là tính chất của trọng tâm tam giác: trọng tâm chia trung tuyến theo tỉ lệ 2:1, nên:
\[
\frac{BD}{BG} = \frac{3}{2},\quad \frac{CE}{CG} = \frac{3}{2}
\]
b) Chứng minh:
- Tổng độ dài \( BD + CE \approx 9.88 \)
- Ba phần hai độ dài \( BC = 1.5 \times BC \approx 9.0 \)
Vì \( BD + CE > \dfrac{3}{2}BC \), ta có điều phải chứng minh.
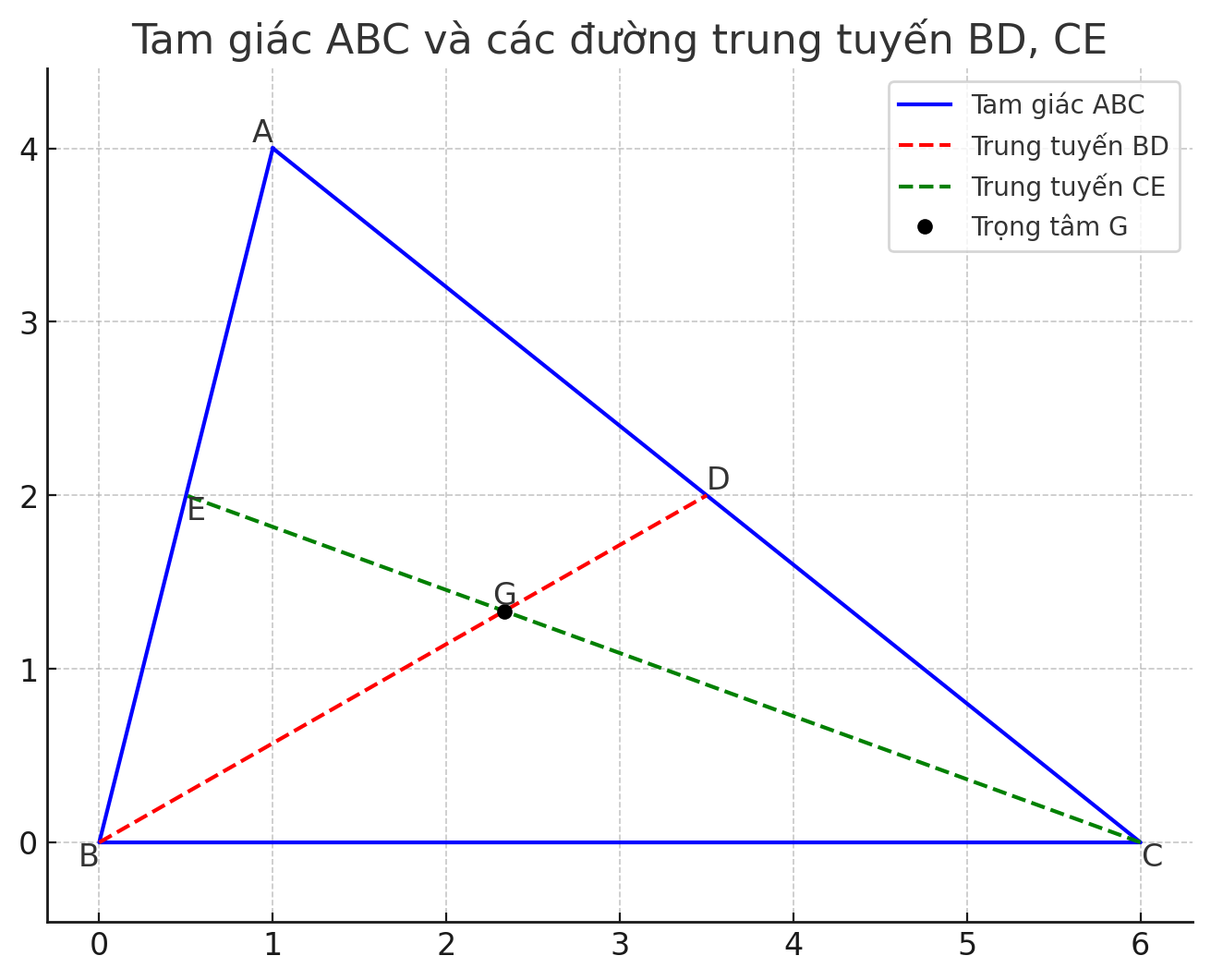
tỉ số BD/BG và CE/CG
Trong tam giác ABC, BD và CE là các đường trung tuyến
G là giao điểm của hai đường trung tuyến BD và CE, nên G là trọng tâm của tam giác ABC
Theo tính chất của trọng tâm trong tam giác nên ta có
BG = (2/3)BD
CG = (2/3)CE
=>
=>
BD/BG = BD / ((2/3)BD) = 3/2
CE/CG = CE / ((2/3)CE) = 3/2
b/
b/
Xét tam giác BGC.
Theo bất đẳng thức tam giác ta có
BG + CG > BC
Thay BG = (2/3)BD và CG = (2/3)CE
(2/3)BD + (2/3)CE > BC
(3/2) * [(2/3)BD + (2/3)CE] > (3/2)BC
BD + CE > (3/2)BC
đã chứng minh được BD + CE > (3/2)BC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669
Gửi báo cáo thành công!


