Cho hình chóp ABCD có đáy ABCD là hình vuông và SA vuông góc (ABCD) . Tính số đo của mỗi góc nhị diện sau : a) [B,SA,D] b) [ B,SA,C]
Quảng cáo
1 câu trả lời 90
a) Góc nhị diện (B,SA,D)
- Xét 2 mặt phẳng:
- (SAB) chứa cạnh SA, SB
- (SAD) chứa cạnh SA, SD
→ Giao tuyến chung là SA
→ Góc nhị diện giữa hai mặt phẳng là góc giữa hai mặt bên SAB và SAD
Góc giữa hai mặt phẳng chính là góc giữa hai đường thẳng nằm trong hai mặt đó và cùng vuông góc với giao tuyến SA
→ Trong mặt đáy, lấy hai đoạn vuông góc SA:
- AB∈(SAB)
- AD∈(SAD)
Mà đáy là hình vuông ⇒ ∠BAD=90∘
→ Vậy góc nhị diện \( (B, SA, D) = \boxed{90^\circ}
b) Góc nhị diện (B,SA,C)
Tương tự:
- Mặt phẳng (SAB) và (SAC), giao nhau theo SA
- Trong mặt đáy, chọn 2 đoạn vuông góc SA:
- AB∈(SAB),
- AC∈(SAC)
Xét góc giữa AB và AC trong đáy hình vuông:
- Tam giác vuông ABC vuông tại A, vì hình vuông có đường chéo AC, BD
→ ∠BAC=45∘
→ Vậy góc nhị diện \( (B, SA, C) = \boxed{45^\circ}
a) ∠(B,SA,D)=90∘
b) ∠(B,SA,C)=45∘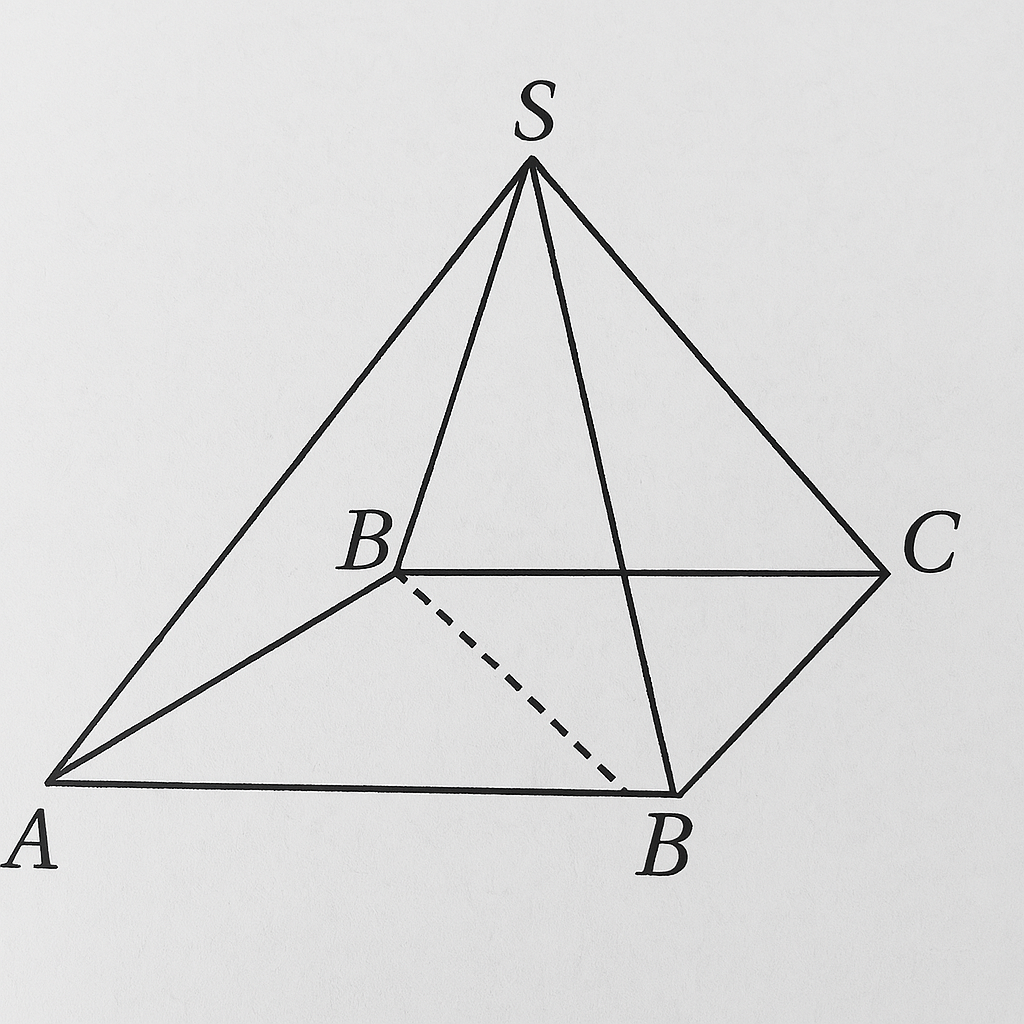
Quảng cáo




![CEO tập đoàn Lục thị[nk]](/upload/images/user/1757779274-anh-chup-man-hinh-2025-09-09-000613png.png)








