Quảng cáo
3 câu trả lời 357
Ta xét tam giác \( ABM \) và \( HBM \):
- \( BM \): chung
- \( \angle ABM = \angle HBM \) (do \( BM \) là phân giác)
- \( AM \perp BC \), \( MH \perp BC \) ⇒ \( AM \parallel MH \)
Nếu \( AM \parallel MH \), cùng bằng chiều cao từ M xuống AB và HC ⇒ AM = MH
Xét tam giác vuông có:
- \( AM \perp BC \), \( MH \perp BC \) ⇒ \( AM = MH \)
- \( \angle ABM = \angle HBM \)
- \( BM \): chung
Hai tam giác \( ABM \) và \( HBM \) có 2 cạnh và góc xen giữa bằng nhau:
\[
\boxed{ \triangle ABM = \triangle HBM \quad (c.g.c) }
\]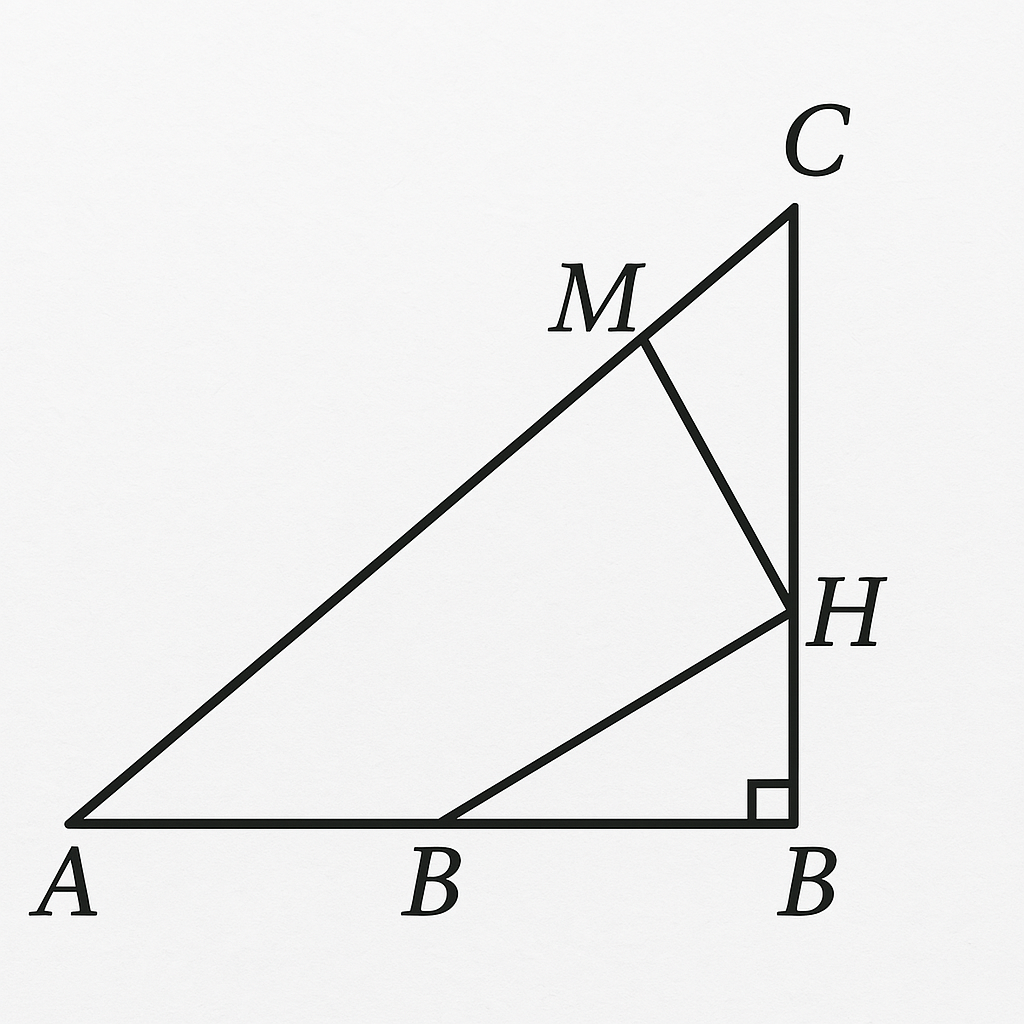
Để chứng minh \( \triangle ABM = \triangle HBM \), ta thực hiện các bước sau:
**a) Chứng minh \(\triangle ABM = \triangle HBM\)**
Xét \(\triangle ABM\) và \(\triangle HBM\) có:
* \( \angle BAM = \angle BHM = 90^\circ \) (do \(\triangle ABC\) vuông tại A và MH vuông góc với BC)
* BM là cạnh chung
* \(\angle ABM = \angle HBM\) (do BM là tia phân giác của góc B)
Vậy, \(\triangle ABM = \triangle HBM\) (cạnh huyền - góc nhọn).
Xét hai tam giác vuông ∆ABM (vuông tại A) và ∆HBM (vuông tại H), ta có:
Do đó, hai tam giác vuông ∆ABM và ∆HBM bằng nhau theo trường hợp cạnh huyền - góc nhọn
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


