Quảng cáo
2 câu trả lời 211
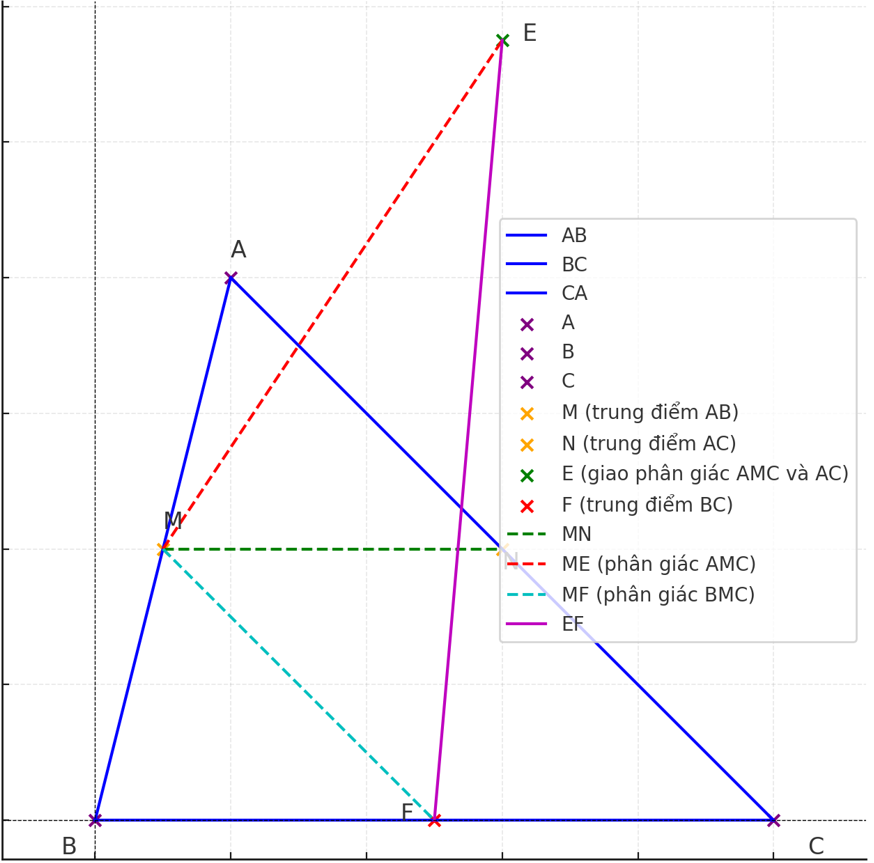
a. Tứ giác MNBC là hình gì?
Vì M và N lần lượt là trung điểm của AB và AC, nên MN là đường trung bình của tam giác ABC. Do đó:
MN song song với BC
MN = 1/2 BC
Vì MN song song với BC, tứ giác MNBC có hai cạnh đối song song, nên MNBC là hình thang.
b. Chứng minh EF song song với AB
Xét tam giác AMC:
ME là tia phân giác của góc AMC nên ta có:AE/EC = AM/MC (tính chất đường phân giác trong tam giác)
Xét tam giác BMC:
MF là tia phân giác của góc BMC nên ta có:BF/FC = BM/MC (tính chất đường phân giác trong tam giác)
Mà:
AM = BM (vì M là trung điểm AB)
Từ đó suy ra:
AE/EC = BF/FC
Áp dụng định lý Ta-lét đảo vào tam giác ABC:
Vì AE/EC = BF/FC nên EF // AB (định lý Ta-lét đảo)
Vậy EF song song với AB
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107742
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68485
Đã trả lời bởi chuyên gia
68485 -
 Đã trả lời bởi chuyên gia
52942
Đã trả lời bởi chuyên gia
52942 -
 Đã trả lời bởi chuyên gia
47433
Đã trả lời bởi chuyên gia
47433 -
 Đã trả lời bởi chuyên gia
45529
Đã trả lời bởi chuyên gia
45529 -
 Đã trả lời bởi chuyên gia
45189
Đã trả lời bởi chuyên gia
45189 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38558
Đã trả lời bởi chuyên gia
38558 -
 Đã trả lời bởi chuyên gia
38279
Đã trả lời bởi chuyên gia
38279


