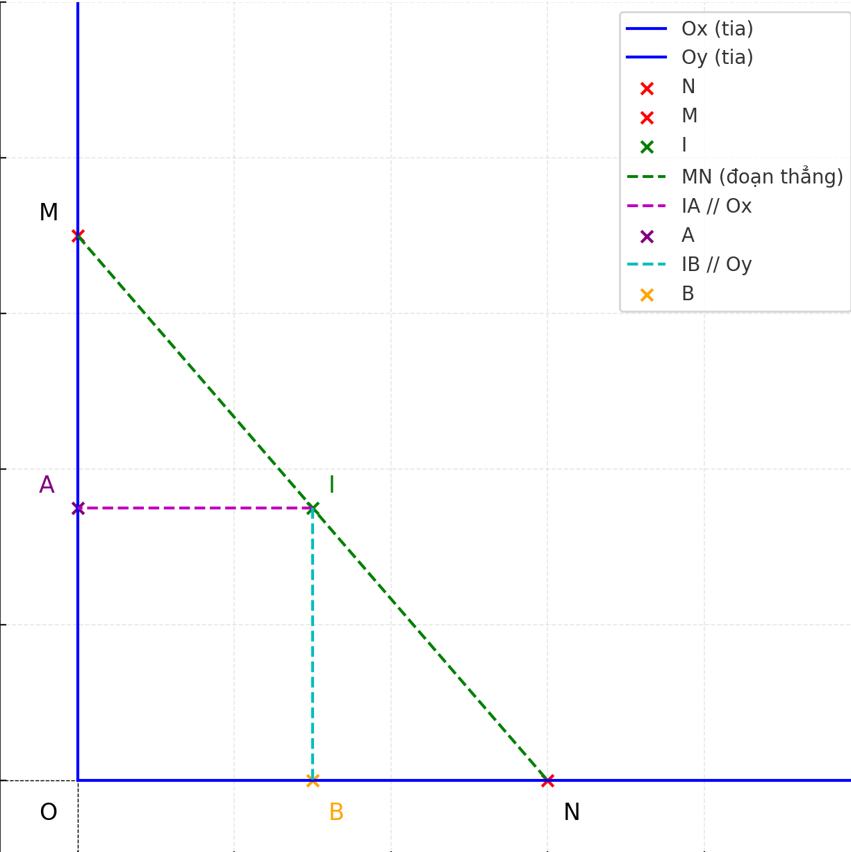
a) Tứ giác OAIB là hình bình hành:

Xét tứ giác OAIB có:

IA // OB (do IA // Ox và B thuộc Ox)
IB // OA (do IB // Oy và A thuộc Oy)
Theo định nghĩa hình bình hành, tứ giác có các cặp cạnh đối song song là hình bình hành.
Vậy tứ giác OAIB là hình bình hành.
b) MA/MO + NB/NO = 1:

Xét tam giác OMN:

Vì IA // ON, theo định lý Ta-lét, ta có: MA/MO = AI/ON
Vì IB // OM, theo định lý Ta-lét, ta có: NB/NO = BI/OM
Từ câu a, OAIB là hình bình hành:

Suy ra AI = OB (cạnh đối hình bình hành)
Suy ra IB = OA (cạnh đối hình bình hành)
Thay AI = OB và IB = OA vào hai tỷ lệ thức trên:

MA/MO = OB/ON (1)
NB/NO = OA/OM (2)
Cộng vế theo vế (1) và (2):

MA/MO + NB/NO = OB/ON + OA/OM
Xét tam giác OMN và tam giác OAB có IB//OM và IA//ON

Áp dụng định lý Ta-let: OB/ON = AB/MN và OA/OM = AB/MN
Suy ra OB/ON = AB/MN và OA/OM = AB/MN
Suy ra: OB/ON + OA/OM = AB/MN + AB/MN = (AB+AB)/MN = 2AB/MN
Xét tam giác OMN, xét điểm I trên MN:

Ta có MI + IN = MN
Vì IB//OM, theo định lý Ta-let: MI/MN = BI/ON
Vì IA//ON, theo định lý Ta-let: IN/MN = IA/OM
Suy ra MI/MN + IN/MN = BI/ON + IA/OM
Mà MI + IN = MN suy ra (MI+IN)/MN = 1 suy ra BI/ON + IA/OM = 1
Mà AI = OB và BI = OA, ta suy ra OA/OM + OB/ON = 1
Do đó:

MA/MO + NB/NO = OB/ON + OA/OM = 1
Vậy MA/MO + NB/NO = 1 (dpcm).

a) Tứ giác OAIB là hình bình hành:

Xét tứ giác OAIB có:

IA // OB (do IA // Ox và B thuộc Ox)
IB // OA (do IB // Oy và A thuộc Oy)
Theo định nghĩa hình bình hành, tứ giác có các cặp cạnh đối song song là hình bình hành.
Vậy tứ giác OAIB là hình bình hành.
b) MA/MO + NB/NO = 1:

Xét tam giác OMN:

Vì IA // ON, theo định lý Ta-lét, ta có: MA/MO = AI/ON
Vì IB // OM, theo định lý Ta-lét, ta có: NB/NO = BI/OM
Từ câu a, OAIB là hình bình hành:

Suy ra AI = OB (cạnh đối hình bình hành)
Suy ra IB = OA (cạnh đối hình bình hành)
Thay AI = OB và IB = OA vào hai tỷ lệ thức trên:

MA/MO = OB/ON (1)
NB/NO = OA/OM (2)
Cộng vế theo vế (1) và (2):

MA/MO + NB/NO = OB/ON + OA/OM
Xét tam giác OMN và tam giác OAB có IB//OM và IA//ON

Áp dụng định lý Ta-let: OB/ON = AB/MN và OA/OM = AB/MN
Suy ra OB/ON = AB/MN và OA/OM = AB/MN
Suy ra: OB/ON + OA/OM = AB/MN + AB/MN = (AB+AB)/MN = 2AB/MN
Xét tam giác OMN, xét điểm I trên MN:

Ta có MI + IN = MN
Vì IB//OM, theo định lý Ta-let: MI/MN = BI/ON
Vì IA//ON, theo định lý Ta-let: IN/MN = IA/OM
Suy ra MI/MN + IN/MN = BI/ON + IA/OM
Mà MI + IN = MN suy ra (MI+IN)/MN = 1 suy ra BI/ON + IA/OM = 1
Mà AI = OB và BI = OA, ta suy ra OA/OM + OB/ON = 1
Do đó:

MA/MO + NB/NO = OB/ON + OA/OM = 1
Vậy MA/MO + NB/NO = 1 (dpcm).