a) Chứng minh tứ giác AECF là hình bình hành
b) Chứng minh tứ giác EOFK là hình chữ nhật
c) Tìm điều kiện cho hình bình hành ABCD để tứ giác EOFK là hình vuông
Quảng cáo
2 câu trả lời 160
a/ AE = 1/2 AB = AD
AD = 1/2 CD = AD
=> AE || DF và AE = DF
=> AEDF là hình bình hành
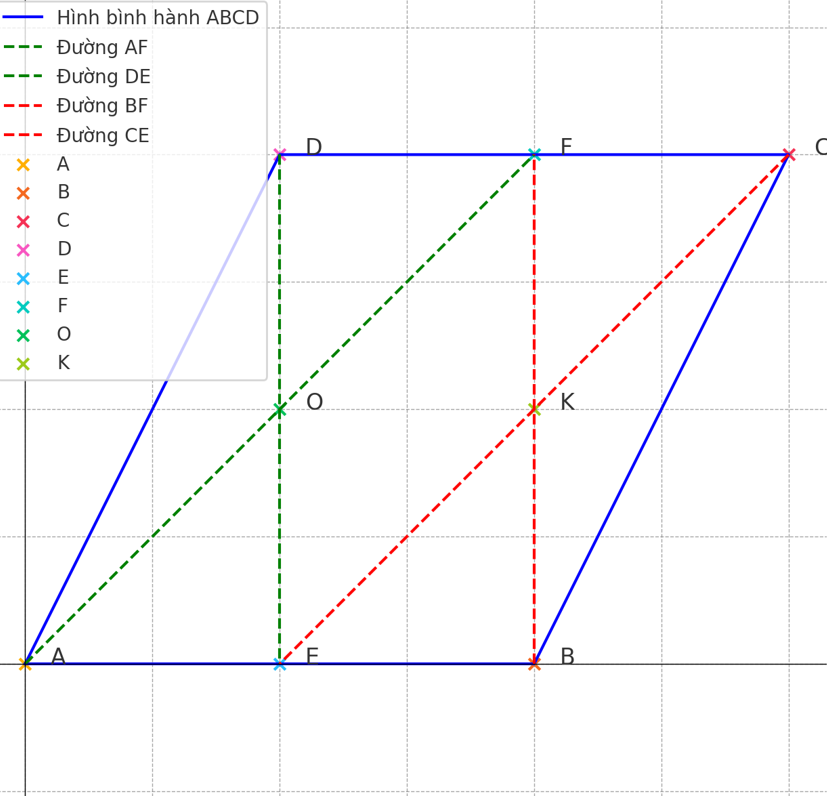
a) Chứng minh tứ giác AECF là hình bình hành:
Xét tứ giác AECF:
E là trung điểm của AB (giả thiết) nên AE = EB = AB/2
F là trung điểm của CD (giả thiết) nên CF = FD = CD/2
ABCD là hình bình hành (giả thiết) nên AB = CD và AB // CD
Suy ra: AE = CF và AE // CF (vì E thuộc AB, F thuộc CD)
Kết luận: Tứ giác AECF có một cặp cạnh đối song song và bằng nhau nên AECF là hình bình hành.
b) Chứng minh tứ giác EOFK là hình chữ nhật:
Chứng minh EOFK là hình bình hành:
AECF là hình bình hành (chứng minh trên) nên AF // CE hay EO // KF (1)
Ta có: AE = FD (cùng bằng 1/2 AB = 1/2 CD), AE // FD (vì AB // CD)
Suy ra AEDF là hình bình hành (dấu hiệu nhận biết)
Do đó: AF // DE hay OF // EK (2)
Từ (1) và (2) suy ra EOFK là hình bình hành (dấu hiệu nhận biết)
Chứng minh EOFK có một góc vuông:
Ta có: AD = BC (ABCD là hình bình hành), AD = 1/2 AB (giả thiết), AB = 2AE (E là trung điểm AB)
Suy ra: AD = AE, do đó tam giác ADE cân tại A
Mà AF // DE (AEDF là hình bình hành)
Suy ra: góc DAE = góc AEO (hai góc đồng vị)
Tam giác ADE cân tại A nên góc ADE = góc AED
Mà góc AEO + góc AED = 180 độ (hai góc kề bù)
Suy ra 2 * góc AED = 180 độ (vì góc ADE = góc AED)
Vậy góc AED = 90 độ
Hay góc EOK = 90 độ (hai góc đối đỉnh)
Kết luận: Hình bình hành EOFK có một góc vuông nên EOFK là hình chữ nhật.
c) Tìm điều kiện cho hình bình hành ABCD để tứ giác EOFK là hình vuông:
EOFK là hình vuông khi và chỉ khi nó vừa là hình chữ nhật vừa là hình thoi.
EOFK đã là hình chữ nhật (chứng minh trên).
Để EOFK là hình thoi thì EO = FO.
Ta có:Tam giác AOE = tam giác DOF (g.c.g) vì:góc AOE = góc DOF (đối đỉnh)
AE = DF (cùng bằng 1/2 AB = 1/2 CD)
góc EAO = góc FDO (so le trong)
Suy ra: OE = OF
Để OE = OF = EO = FO thì tam giác AOE phải là tam giác vuông cân tại O.
Khi đó, góc AEO = 45 độ.
Mà góc AEO = góc DAE (hai góc đồng vị)
Suy ra góc DAE = 45 độ.
Lại có: góc ADE = góc AED = 90 độ / 2 = 45 độ (vì tam giác ADE cân tại A)
Suy ra góc DAB = góc DAE + góc EAB = 45 độ + 45 độ = 90 độ
=> Để EOFK là hình vuông thì hình bình hành ABCD phải có góc A = 90 độ, tức là ABCD phải là hình chữ nhật và có AB = 2AD
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


