Bài 2:Cho `triangleABC` vuông tại `A`,tia phân giác `hatB` cắt cạnh `AC` tại `M`,kẻ `MD bot BC` tại `D`.
a,Chứng minh `hat(BMA)=hat(BMD)`
b,Gọi `E` là giao điểm của hai đường thẳng `MD` và `BA`. Chứng minh `AC=DE`.
c, Chứng minh `triangleAME=triangleDMC`.
d, Kẻ `DK bot MC` tại `H` và `AK bot ME` tại `K`, hai tia `DH` và `AK` cắt nhau
tại `N`. Chứng minh `MN` là phân giác `hat(KMH)`.
e, Chứng minh `3` điểm `B, M, N` thẳng hàng.
f, Chứng minh `BN bot AD,BN bot EC`.
g, Giả sử `hat(ABC)=60^@`, khi đó `triangleAND` là tam giác gì? Chứng minh?
Quảng cáo
2 câu trả lời 244
a) Chứng minh BMA =BMD
Xét ΔBAM và ΔBDM có:BAM =BDM =90∘ (giả thiết)
BM là cạnh chung
ABM =DBM (BM là tia phân giác góc B)
Suy ra: ΔBAM = ΔBDM (cạnh huyền - góc nhọn)
Kết luận: BMA =BMD (hai góc tương ứng)
b) Gọi E là giao điểm của hai đường thẳng MD và BA. Chứng minh AC = DE.
Xét ΔBAM và ΔBEM có:BAM =BEM =90∘
BM là cạnh chung
ABM =EBM (BM là tia phân giác góc B)
Suy ra: ΔBAM = ΔBEM (cạnh huyền - góc nhọn)
Suy ra: BA = BE (hai cạnh tương ứng)
Xét ΔBAC và ΔBED có:BAC =BED =90∘
BA = BE (chứng minh trên)
ABC chung
Suy ra: ΔBAC = ΔBED (góc - cạnh - góc)
Kết luận: AC = DE (hai cạnh tương ứng)
c) Chứng minh Δ AME = Δ DMC.
Từ câu b: ΔBAC = ΔBED => AC = DE
Mà: BA = BE (chứng minh trên)
Suy ra: BE - BA = BD - BC hay AE = DC
Từ câu b: ΔBAM = ΔBEM => AM = EM (hai cạnh tương ứng)
Từ câu a: ΔBAM = ΔBDM => AM = DM (hai cạnh tương ứng)
Suy ra AM = DM
Xét ΔAME và ΔDMC có:AM = DM (chứng minh trên)
AE = DC (chứng minh trên)
MAE =MDC =90∘
Suy ra: ΔAME = ΔDMC (cạnh - góc - cạnh)
Kết luận: ΔAME = ΔDMC
d) Kẻ DK ⊥ MC tại H và AK ⊥ ME tại K, hai tia DH và AK cắt nhau tại N. Chứng minh MN là phân giác KMH .
Xét ΔMKA và ΔMHD có:MKA =MHD =90∘ (giả thiết)
MA = MD (chứng minh trên)
AMK =DMH (hai góc đối đỉnh)
Suy ra: ΔMKA = ΔMHD (cạnh huyền - góc nhọn)
Suy ra: MK = MH (hai cạnh tương ứng)
Xét ΔMNK và ΔMNH có:MK = MH (chứng minh trên)
MN là cạnh chung
MKN =MHN =90∘ (vì ΔMKA = ΔMHD)
Suy ra: ΔMNK = ΔMNH (cạnh huyền - cạnh góc vuông)
Suy ra: KMN =HMN (hai góc tương ứng)
Kết luận: MN là phân giác KMH
e) Chứng minh 3 điểm B, M, N thẳng hàng.
Từ câu d: ΔMNK = ΔMNH => NK = NH
Xét ΔANK và ΔANH có:AK = AH (ΔMKA = ΔMHD)
NK = NH (chứng minh trên)
AN là cạnh chung
Suy ra: ΔANK = ΔANH (cạnh - cạnh - cạnh)
Suy ra: ANK =ANH (hai góc tương ứng)
Mà: ANK +ANH =180∘ (hai góc kề bù)
Suy ra: ANK =ANH =90∘
Suy ra: AN ⊥ KH
Mặt khác BM là phân giác góc B của tam giác ABC, mà tam giác ABC vuông tại A => BM cũng là đường cao của tam giác ABC. Từ đó ta có BM ⊥ AC.
Mà N thuộc AK, mà AK vuông góc với ME => N thuộc đường cao từ A xuống ME.
Mà B, M, N đều thuộc đường thẳng BM => B, M, N thẳng hàng
f) Chứng minh BN ⊥ AD, BN ⊥ EC.
Từ câu e: B, M, N thẳng hàng.
Từ câu a: ΔBAM = ΔBDM => BAM =BDM =90∘ => BD ⊥ AD
Mà: BM là phân giác góc B => BN là phân giác góc B
Mà: ABD là góc ngoài của tam giác ABC => BN ⊥ AD
Chứng minh tương tự: BN ⊥ EC
g) Giả sử ABC = 60°, khi đó Δ AND là tam giác gì? Chứng minh?
Nếu ABC =60∘
Mà BM là phân giác ABC => ABM =MBD =30∘
Xét ΔABD có: BAD =90∘, ABD =60∘ => ADB =30∘
Mà: BN ⊥ AD => ANB =DNB =90∘
Xét ΔABN có: BAN =90∘, ABN =30∘ => ANB =60∘
Xét ΔDBN có: BDN =90∘, DBN =30∘ => DNB =60∘
Xét ΔAND có:NAD =90∘−60∘=30∘
NDA =90∘−60∘=30∘
AND =180−30−30=120 => Không thể là tam giác đều
Mà AN = DN (chứng minh trên)
Kết luận: ΔAND là tam giác cân tại N (AN = DN) và có AND =120∘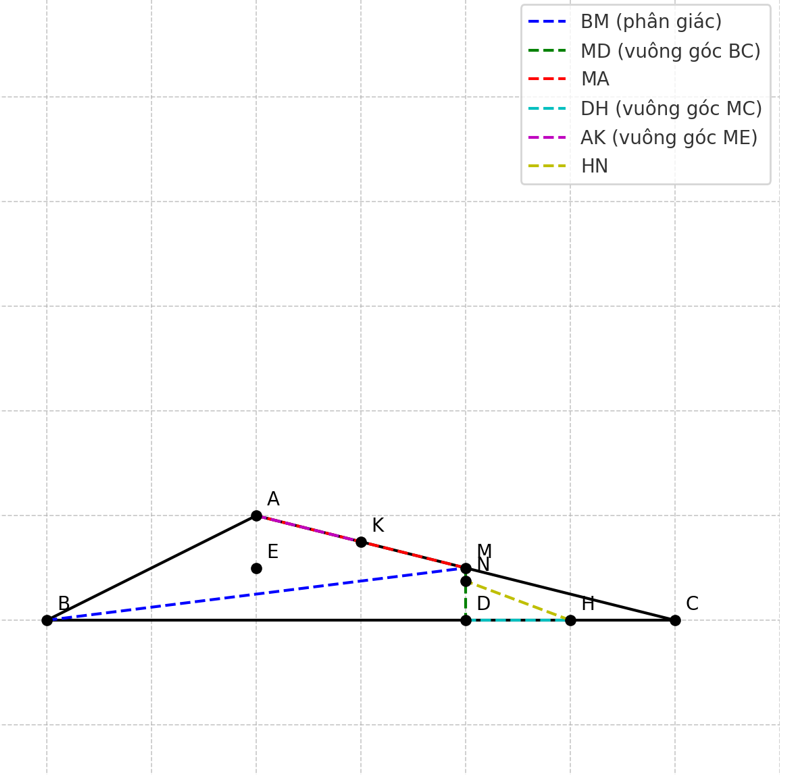
a) Chứng minh BMA =BMD
Xét ΔBAM và ΔBDM có:BAM =BDM =90∘ (giả thiết)
BM là cạnh chung
ABM =DBM (BM là tia phân giác góc B)
Suy ra: ΔBAM = ΔBDM (cạnh huyền - góc nhọn)
Kết luận: BMA =BMD (hai góc tương ứng)
b) Gọi E là giao điểm của hai đường thẳng MD và BA. Chứng minh AC = DE.
Xét ΔBAM và ΔBEM có:BAM =BEM =90∘
BM là cạnh chung
ABM =EBM (BM là tia phân giác góc B)
Suy ra: ΔBAM = ΔBEM (cạnh huyền - góc nhọn)
Suy ra: BA = BE (hai cạnh tương ứng)
Xét ΔBAC và ΔBED có:BAC =BED =90∘
BA = BE (chứng minh trên)
ABC chung
Suy ra: ΔBAC = ΔBED (góc - cạnh - góc)
Kết luận: AC = DE (hai cạnh tương ứng)
c) Chứng minh Δ AME = Δ DMC.
Từ câu b: ΔBAC = ΔBED => AC = DE
Mà: BA = BE (chứng minh trên)
Suy ra: BE - BA = BD - BC hay AE = DC
Từ câu b: ΔBAM = ΔBEM => AM = EM (hai cạnh tương ứng)
Từ câu a: ΔBAM = ΔBDM => AM = DM (hai cạnh tương ứng)
Suy ra AM = DM
Xét ΔAME và ΔDMC có:AM = DM (chứng minh trên)
AE = DC (chứng minh trên)
MAE =MDC =90∘
Suy ra: ΔAME = ΔDMC (cạnh - góc - cạnh)
Kết luận: ΔAME = ΔDMC
d) Kẻ DK ⊥ MC tại H và AK ⊥ ME tại K, hai tia DH và AK cắt nhau tại N. Chứng minh MN là phân giác KMH .
Xét ΔMKA và ΔMHD có:MKA =MHD =90∘ (giả thiết)
MA = MD (chứng minh trên)
AMK =DMH (hai góc đối đỉnh)
Suy ra: ΔMKA = ΔMHD (cạnh huyền - góc nhọn)
Suy ra: MK = MH (hai cạnh tương ứng)
Xét ΔMNK và ΔMNH có:MK = MH (chứng minh trên)
MN là cạnh chung
MKN =MHN =90∘ (vì ΔMKA = ΔMHD)
Suy ra: ΔMNK = ΔMNH (cạnh huyền - cạnh góc vuông)
Suy ra: KMN =HMN (hai góc tương ứng)
Kết luận: MN là phân giác KMH
e) Chứng minh 3 điểm B, M, N thẳng hàng.
Từ câu d: ΔMNK = ΔMNH => NK = NH
Xét ΔANK và ΔANH có:AK = AH (ΔMKA = ΔMHD)
NK = NH (chứng minh trên)
AN là cạnh chung
Suy ra: ΔANK = ΔANH (cạnh - cạnh - cạnh)
Suy ra: ANK =ANH (hai góc tương ứng)
Mà: ANK +ANH =180∘ (hai góc kề bù)
Suy ra: ANK =ANH =90∘
Suy ra: AN ⊥ KH
Mặt khác BM là phân giác góc B của tam giác ABC, mà tam giác ABC vuông tại A => BM cũng là đường cao của tam giác ABC. Từ đó ta có BM ⊥ AC.
Mà N thuộc AK, mà AK vuông góc với ME => N thuộc đường cao từ A xuống ME.
Mà B, M, N đều thuộc đường thẳng BM => B, M, N thẳng hàng
f) Chứng minh BN ⊥ AD, BN ⊥ EC.
Từ câu e: B, M, N thẳng hàng.
Từ câu a: ΔBAM = ΔBDM => BAM =BDM =90∘ => BD ⊥ AD
Mà: BM là phân giác góc B => BN là phân giác góc B
Mà: ABD là góc ngoài của tam giác ABC => BN ⊥ AD
Chứng minh tương tự: BN ⊥ EC
g) Giả sử ABC = 60°, khi đó Δ AND là tam giác gì? Chứng minh?
Nếu ABC =60∘
Mà BM là phân giác ABC => ABM =MBD =30∘
Xét ΔABD có: BAD =90∘, ABD =60∘ => ADB =30∘
Mà: BN ⊥ AD => ANB =DNB =90∘
Xét ΔABN có: BAN =90∘, ABN =30∘ => ANB =60∘
Xét ΔDBN có: BDN =90∘, DBN =30∘ => DNB =60∘
Xét ΔAND có:NAD =90∘−60∘=30∘
NDA =90∘−60∘=30∘
AND =180−30−30=120 => Không thể là tam giác đều
Mà AN = DN (chứng minh trên)
Kết luận: ΔAND là tam giác cân tại N (AN = DN) và có AND =120∘
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


