Quảng cáo
1 câu trả lời 551
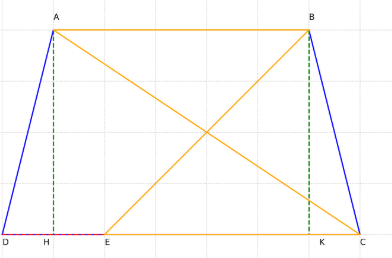
Chứng minh tứ giác ABKH là hình chữ nhật
Trong hình thang cân ABCD, hai đáy AB và CD song song (AB // CD).
Các đường cao AH và BK vuông góc với CD, do đó AH ⊥ CD và BK ⊥ CD.
Vì AB // CD và AH ⊥ CD, suy ra AH ⊥ AB. Tương tự, BK ⊥ AB.
Như vậy, trong tứ giác ABKH, các góc tại A và B đều là góc vuông.
Do đó, tứ giác ABKH có hai cạnh đối song song và các góc vuông, nên ABKH là hình chữ nhật.
2. Chứng minh DH = CK
Xét hai tam giác vuông ADH và BCK:
AD = BC (vì ABCD là hình thang cân, hai cạnh bên bằng nhau).
AH = BK (cùng là đường cao của hình thang cân).
Do đó, hai tam giác ADH và BCK bằng nhau theo trường hợp cạnh - góc - cạnh.
Suy ra, DH = CK (các cạnh tương ứng).
3. Gọi E là điểm đối xứng với D qua H. Chứng minh tứ giác ABCE là hình bình hành
Vì E đối xứng với D qua H, nên H là trung điểm của DE và HE = HD.
Đã chứng minh DH = CK, do đó HE = CK.
Trong tứ giác ABCE:
AB // CE (vì AB // CD và E đối xứng với D qua H).
AB = CE (vì AB = CD và E đối xứng với D qua H).
=> tứ giác ABCE có một cặp cạnh đối song song và bằng nhau, nên ABCE là hình bình hành
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


