Bước 1: Xác định số đo góc giữa A và B Mặt đồng hồ được chia thành 12 giờ, mỗi giờ tương ứng với một góc:

              Góc giữa số 2 và số 9 trên đồng hồ được tính bằng số giờ cách nhau:

        Vậy số đo góc giữa A và B là:

Bước 2: Tính chu vi của đường tròn Đường kính của đường tròn là d = 60 cm, do đó chu vi của đường tròn là:

Bước 3: Tính độ dài cung nhỏ  Độ dài cung tròn được tính bằng công thức:

          Thay $\theta = 210°$ và C = 60$\mathrm{\pi }$ vào công thức:

              Rút gọn:

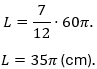
Bước 4: Tính giá trị gần đúng Sử dụng $\mathrm{\pi } \approx 3.1416$, ta có:

Kết luận: Độ dài cung nhỏ AB là:

              (làm tròn đến hàng phần trăm).

Để tính độ dài cung nhỏ \( AB \) của đường tròn, ta cần biết một vài thông tin:

1. **Đường kính của đồng hồ**: 60 cm, do đó bán kính \( r \) = \( \frac{60}{2} = 30 \) cm.
2. **Vị trí các số trên đồng hồ**: Số 2 và số 9 tương ứng với các vị trí trên mặt đồng hồ.

### Tính số độ giữa các số
– Trên mặt đồng hồ, mỗi số cách nhau 30 độ (360 độ / 12 số = 30 độ).

– Số 2 và số 9 cách nhau:

\[
\text{Số vị trí giữa 2 và 9} = 9 - 2 = 7 \text{ vị trí}
\]

– Do đó, góc giữa điểm A (số 2) và B (số 9) là:

\[
\theta = 7 \times 30^\circ = 210^\circ
\]

### Tính độ dài cung nhỏ AB
Công thức tính độ dài cung là:

\[
L = \frac{\theta}{360^\circ} \times 2\pi r
\]

Thay các giá trị vào công thức:

\[
L = \frac{210^\circ}{360^\circ} \times 2\pi \times 30
\]

Giải các bước:

1. Tính \( \frac{210}{360} \):

\[
\frac{210}{360} = \frac{7}{12}
\]

2. Tính \( L \):

\[
L = \frac{7}{12} \times 2\pi \times 30 = \frac{7 \times 60\pi}{12} = 35\pi
\]

3. Tính độ dài \( L \) theo số gần đúng của \( \pi \):

\[
L \approx 35 \times 3.14 \approx 109.9 \text{ cm}
\]

### Kết luận
Khoảng độ dài cung nhỏ \( AB \) là khoảng **109.9 cm**.