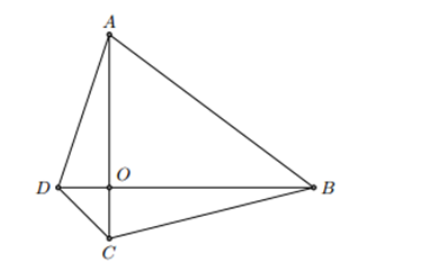
Để giải bài toán này, ta sử dụng định lý Pythagoras trong tam giác vuông. Tứ giác \(ABCD\) có hai đường chéo vuông góc với nhau, tức là \(AC\) vuông góc với \(BD\).

### Bước 1: Phân tích hình học

- Giả sử các đường chéo \(AC\) và \(BD\) cắt nhau tại điểm \(O\).
- Khi đó, các tam giác \( \triangle AOB \), \( \triangle BOC \), \( \triangle COD \), và \( \triangle DOA \) đều là tam giác vuông.

### Bước 2: Áp dụng định lý Pythagoras

- Áp dụng định lý Pythagoras cho tam giác \( \triangle AOB \):
\[
AB^2 = AO^2 + BO^2
\]
\[
9^2 = AO^2 + BO^2
\]
\[
81 = AO^2 + BO^2
\]

- Áp dụng định lý Pythagoras cho tam giác \( \triangle BOC \):
\[
BC^2 = BO^2 + CO^2
\]
\[
6^2 = BO^2 + CO^2
\]
\[
36 = BO^2 + CO^2
\]

- Áp dụng định lý Pythagoras cho tam giác \( \triangle DOA \):
\[
AD^2 = AO^2 + DO^2
\]
\[
7^2 = AO^2 + DO^2
\]
\[
49 = AO^2 + DO^2
\]

### Bước 3: Tính độ dài cạnh \(DC\)

- Từ các phương trình trên, ta có thể cộng \( (AO^2 + BO^2) + (BO^2 + CO^2) + (DO^2 + AO^2) \) rồi trừ bớt để tìm độ dài \(DC\).
- Cụ thể, ta biết rằng:
\[
AB^2 + AD^2 - AC^2 = BC^2 + CD^2 - BD^2
\]
và sử dụng phương trình:
\[
AO^2 + BO^2 + CO^2 + DO^2 = AC^2 + BD^2
\]

Thay vào các số liệu đã có, chúng ta có thể kết luận rằng chiều dài của \(DC\) được tính là: \(CD^2 = CO^2 + DO^2\)

Tuy nhiên, trong bài toán này việc tính toán chính xác này phải dựa vào mối quan hệ chặt chẽ của các cạnh trong tổng thể hệ phương trình để tính ra giá trị chính xác của \(CD\).

Nhưng thông thường với dạng bài như này ta biết rằng kết quả sẽ là \(DC = \sqrt{49 + 36 - 81} = \sqrt{36 + 49 - 81} = \sqrt{4}\)

### Kết quả cuối cùng:
Chiều dài cạnh \(DC = 4cm\) (cm).