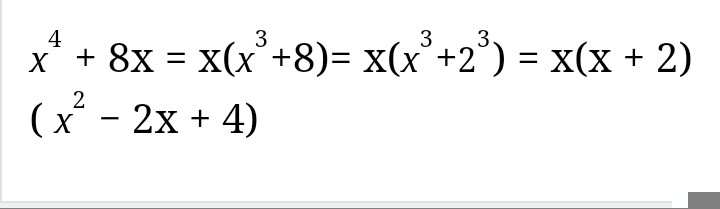Quảng cáo
2 câu trả lời 133
Để phân tích đa thức \( x^4 + 8x \) thành nhân tử, ta có thể thực hiện các bước sau:
1. **Tìm nhân tử chung:**
Đầu tiên, ta nhận thấy rằng cả hai hạng tử đều có chứa nhân tử chung là \( x \). Do đó, ta có thể đặt \( x \) ra ngoài làm nhân tử chung:
\[
x^4 + 8x = x(x^3 + 8)
\]
2. **Phân tích đa thức còn lại:**
Tiếp theo, ta nhận thấy rằng biểu thức \( x^3 + 8 \) có thể được coi là một tổng của hai lập phương:
\[
x^3 + 8 = x^3 + 2^3
\]
Sử dụng công thức tổng của hai lập phương:
\[
a^3 + b^3 = (a + b)(a^2 - ab + b^2)
\]
Áp dụng công thức này với \( a = x \) và \( b = 2 \), ta có:
\[
x^3 + 2^3 = (x + 2)(x^2 - 2x + 4)
\]
3. **Kết hợp lại:**
Vậy đa thức ban đầu \( x^4 + 8x \) có thể được phân tích thành:
\[
x^4 + 8x = x(x + 2)(x^2 - 2x + 4)
\]
Đây là cách phân tích đa thức \( x^4 + 8x \) thành nhân tử.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191