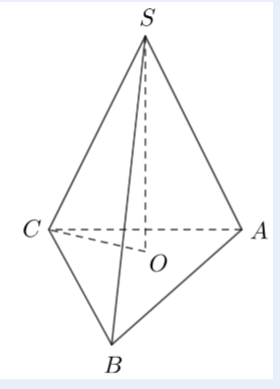
Để tính số đo của góc nhị diện \([A, SC, B]\) trong hình chóp đều \(S.ABC\) với cạnh đáy \(AB = a\) và cạnh bên \(SA = 2a\), ta có thể thực hiện theo các bước sau:

### 1. Xác định tọa độ các điểm trong không gian

Ta đặt hệ tọa độ như sau:

- Chọn điểm \( A \) là gốc tọa độ \( (0,0,0) \).
- Điểm \( B \) sẽ có tọa độ \( (a,0,0) \) (vì \(AB = a\)).
- Vì hình chóp đều có đáy là hình vuông, ta cần xác định tọa độ của điểm \( C \):
- Tọa độ của điểm \( C \) là \( (a,a,0) \) (do \(BC = a\) và điểm \(C\) nằm trên mặt phẳng \(z = 0\)).

- Để xác định tọa độ của điểm \( S \), ta biết rằng \(SA = 2a\) và \(S\) nằm trên mặt phẳng vuông góc với mặt đáy tại trung điểm của \(AB\). Trung điểm của \(AB\) là \( \left(\frac{a}{2}, 0, 0\right) \).

- Sử dụng định lý Pythagoras trong tam giác vuông \(SAB\):
\[
SA^2 = \left(\frac{a}{2}\right)^2 + \left(\frac{a}{2}\right)^2 + h^2
\]
\[
(2a)^2 = \frac{a^2}{4} + \frac{a^2}{4} + h^2
\]
\[
4a^2 = \frac{a^2}{2} + h^2
\]
\[
h^2 = 4a^2 - \frac{a^2}{2} = \frac{8a^2 - a^2}{2} = \frac{7a^2}{2}
\]
\[
h = \sqrt{\frac{7a^2}{2}} = \frac{a \sqrt{7}}{\sqrt{2}} = \frac{a \sqrt{14}}{2}
\]

- Tọa độ của điểm \( S \) là \(\left(\frac{a}{2}, \frac{a}{2}, \frac{a \sqrt{14}}{2}\right)\).

### 2. Tính vector

- Vector \( \overrightarrow{SA} \) từ \( S \) đến \( A \) là:
\[
\overrightarrow{SA} = \left(-\frac{a}{2}, -\frac{a}{2}, -\frac{a \sqrt{14}}{2}\right)
\]

- Vector \( \overrightarrow{SB} \) từ \( S \) đến \( B \) là:
\[
\overrightarrow{SB} = \left(\frac{a}{2}, -\frac{a}{2}, -\frac{a \sqrt{14}}{2}\right)
\]

### 3. Tính góc giữa hai vector

- Tính tích vô hướng của hai vector:
\[
\overrightarrow{SA} \cdot \overrightarrow{SB} = \left(-\frac{a}{2}\right)\left(\frac{a}{2}\right) + \left(-\frac{a}{2}\right)\left(-\frac{a}{2}\right) + \left(-\frac{a \sqrt{14}}{2}\right)\left(-\frac{a \sqrt{14}}{2}\right)
\]
\[
\overrightarrow{SA} \cdot \overrightarrow{SB} = -\frac{a^2}{4} + \frac{a^2}{4} + \frac{a^2 \cdot 14}{4} = \frac{14a^2}{4} = \frac{7a^2}{2}
\]

- Tính độ dài của từng vector:
\[
|\overrightarrow{SA}| = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{a}{2}\right)^2 + \left(-\frac{a \sqrt{14}}{2}\right)^2} = \sqrt{\frac{a^2}{4} + \frac{a^2}{4} + \frac{14a^2}{4}} = \sqrt{\frac{16a^2}{4}} = 2a
\]
\[
|\overrightarrow{SB}| = \sqrt{\left(\frac{a}{2}\right)^2 + \left(-\frac{a}{2}\right)^2 + \left(-\frac{a \sqrt{14}}{2}\right)^2} = \sqrt{\frac{a^2}{4} + \frac{a^2}{4} + \frac{14a^2}{4}} = 2a
\]

- Tính cos của góc giữa hai vector:
\[
\cos \theta = \frac{\overrightarrow{SA} \cdot \overrightarrow{SB}}{|\overrightarrow{SA}| \cdot |\overrightarrow{SB}|} = \frac{\frac{7a^2}{2}}{2a \cdot 2a} = \frac{\frac{7a^2}{2}}{4a^2} = \frac{7}{8}
\]

- Số đo của góc giữa hai vector là:
\[
\theta = \cos^{-1} \left(\frac{7}{8}\right)
\]

**Kết luận:** Số đo của góc nhị diện \([A, SC, B]\) là \(\cos^{-1} \left(\frac{7}{8}\right)\).