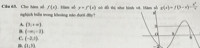Để giải bài toán này, ta cần phân tích hàm số \( g(x) = f(3 - x) - \frac{x^2}{2} \) dựa trên đồ thị của hàm số \( y = f'(x) \), hàm số đạo hàm của hàm \( f(x) \). Dưới đây là các bước để tìm hiểu về hàm \( g(x) \):

### 1. Hiểu đồ thị của \( y = f'(x) \)

- **Đồ thị của \( y = f'(x) \)** cung cấp thông tin về đạo hàm của hàm số \( f(x) \), tức là về độ dốc và sự thay đổi của hàm số \( f(x) \).
- Từ đồ thị của \( y = f'(x) \), chúng ta có thể xác định các điểm cực trị và sự thay đổi của hàm số \( f(x) \) bằng cách tích phân đạo hàm \( f'(x) \).

### 2. Phân tích hàm số \( g(x) = f(3 - x) - \frac{x^2}{2} \)

Để phân tích hàm số \( g(x) \), chúng ta cần:

1. **Xác định đạo hàm của \( g(x) \):**

Hàm số \( g(x) \) bao gồm hai thành phần: \( f(3 - x) \) và \( -\frac{x^2}{2} \). Ta cần tính đạo hàm của từng thành phần:

- Đạo hàm của \( f(3 - x) \):
\[
\frac{d}{dx}[f(3 - x)] = f'(3 - x) \cdot (-1) = -f'(3 - x)
\]

- Đạo hàm của \( -\frac{x^2}{2} \):
\[
\frac{d}{dx}\left(-\frac{x^2}{2}\right) = -x
\]

Do đó, đạo hàm của \( g(x) \) là:
\[
g'(x) = -f'(3 - x) - x
\]

2. **Tìm cực trị và tính toán đồ thị:**

Để tìm cực trị của hàm \( g(x) \), ta giải phương trình \( g'(x) = 0 \):
\[
-f'(3 - x) - x = 0
\]
\[
f'(3 - x) = -x
\]

Phương trình này cho biết các điểm \( x \) mà tại đó hàm số \( g(x) \) có thể có cực trị.

3. **Vẽ đồ thị của \( g(x) \):**

- **Dịch chuyển trục:** Hàm \( f(3 - x) \) là phiên bản đối xứng của \( f(x) \) qua đường thẳng \( x = 3 \), tức là dịch chuyển trục \( x \) sang bên trái 3 đơn vị.
- **Thay đổi độ dốc:** Hàm số \( -\frac{x^2}{2} \) là một hàm bậc 2 có đồ thị là một parabola mở xuống, làm giảm giá trị của hàm số \( g(x) \) theo dạng parabol.

### Ví dụ cụ thể

Giả sử đồ thị của \( y = f'(x) \) cho chúng ta các điểm cực trị và thay đổi của đạo hàm. Ta có thể thực hiện các bước sau để vẽ đồ thị của \( g(x) \):

1. **Tìm các điểm cực trị của \( f(x) \) bằng cách sử dụng \( f'(x) \) và so sánh với \( f'(3 - x) \).**

2. **Tính toán giá trị của \( g(x) \) tại các điểm quan trọng (cực trị của \( f(x) \) và các điểm quan tâm khác).**

3. **Vẽ đồ thị của \( g(x) \) bằng cách dịch chuyển và điều chỉnh đồ thị của \( f(x) \), sau đó cộng với phần parabol từ \( -\frac{x^2}{2} \).**

Hy vọng những hướng dẫn này giúp bạn hiểu và vẽ được đồ thị của hàm số \( g(x) \)! Nếu bạn có đồ thị cụ thể của \( y = f'(x) \), bạn có thể sử dụng các thông tin từ đó để phân tích chính xác hơn.